このページでは、倍率器と分流器について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の理論科目で、実際に出題された倍率器と分流器の過去問題の解き方も解説しています。
倍率器と分流器
直流電圧や電流の計測は、一般的には可動コイル形計器を使って測定します。可動コイル形計器で直接流せる電流は数十[mA]程度ですので、測定の範囲を拡大するために「倍率器」や「分流器」を用います。通常は、電圧で 1000V以下、電流で 30A以下の計器には、倍率器や分流器は内蔵されています。
倍率器とは
電圧計の測定範囲を広げる為に電圧計と直列に接続した抵抗のことを倍率器といいます。倍率器の抵抗を $R_m$、電圧計の内部抵抗を $R_v$、測定電圧を $V$、計器電圧を $v$ とすると、
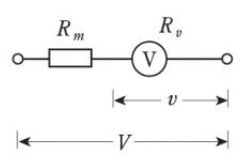
$v=\displaystyle\frac{R_v}{R_m+R_v}V$
ここで、測定回路の電流を $I$ とすると、$V=(R_m+R_v)I$ ですので、倍率器の抵抗値 $R_m$ は、
$R_m=\displaystyle\frac{V}{I}-R_v$
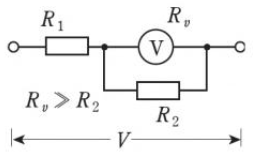
また、高電圧の計測には「分圧器」を用いて電圧計に加わる電圧を低減します。
分流器とは
電流計の測定範囲を広げる為に電流計と並列に接続した抵抗(シャント抵抗)のことを分流器といいます。分流器の抵抗を $R_s$、電流計の内部抵抗を $R_a$、回路電流を $I$、計器電流を $i$ とすると、
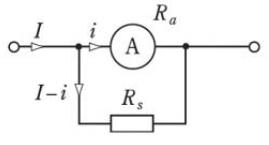
$i=\displaystyle\frac{R_s}{R_s+R_a}I$
ここで、$iR_a=(I-i)R_s$ ですので、分流器の抵抗を $R_s$ は、
$R_s=\displaystyle\frac{i}{I-i}R_a$
電位差計
電位差計は、零位法の原理を用いた測定器で、直流電圧を標準電池の起電力と比較して計測します。滑り抵抗器を動かして、検流計Gの振れがゼロになったときが平衡状態となり、標準電圧 $V_s$ と、未知の電圧 $V_o$ は次のような関係になります。
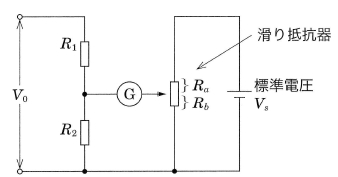
平衡時:$\displaystyle\frac{R_2}{R_1+R_2}V_o=\displaystyle\frac{R_b}{R_a+R_b}V_s$
電験三種-理論(電気・電子計測)過去問題
1999年(平成11年)問4
内部抵抗 3 [kΩ]、最大目盛 1 [V] の電圧計を利用して最大 100 [V] まで測定できるようにするために必要な倍率器の抵抗 [kΩ] として、正しい値は次のうちどれか。
(1) 290 (2) 297 (3) 300 (4) 303 (5) 330
1999年(平成11年)問4 過去問解説
問いを図で示します。
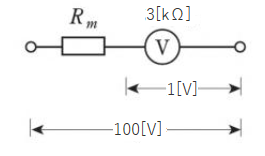
$1=\displaystyle\frac{3×10^3}{R_m+3×10^3}×100$
$R_m+3×10^3=300×10^3$
$R_m=297×10^3$ [Ω]
答え (2)
2003年(平成15年)問17
図1のように、定格電流 1 [mA]、内部抵抗 Rm=23 [Ω] の電流計と抵抗 Rs [Ω] の抵抗で構成された定格電圧5[V]の電圧計がある。 次の(a)及び(b)に答よ。
ただし、電圧計として用いる電流計の目盛り 0~1 [mA] は、0~5 [V] に読み替えるものとし、電圧計の端子aは正極とする。
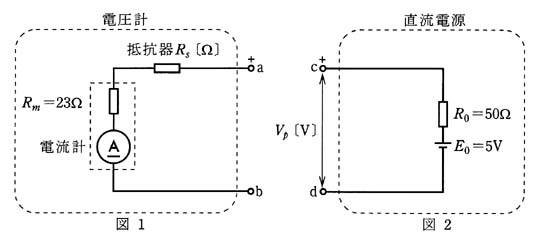
(a) この抵抗器の Rs [Ω] の値として、正しいものは次のうちどれか。
(1) 4947 (2) 4960 (3) 4977 (4) 5000 (5) 5023
(b) 図2のような電圧 E0=5 [V]、内部抵抗 R0=50 [Ω] の直流電源の端子c、dに、この電圧計の端子a、bをそれぞれ接続し、電圧 Vp [V] を測定した。電圧計が指示した Vp [V] の値として、最も近いのは次のうちどれか。
(1) 4.90 (2) 4.95 (3) 4.97 (4) 5.00 (5) 5.02
2003年(平成15年)問17 過去問解説
(a) 図1の端子abに 5 [V] の電圧を加えると、1 [mA] の電流が流れますので、
$R_m+R_s=\displaystyle\frac{5}{1×10^{-3}}$
$23+R_s=5000$
$R_s=4977$ [Ω]
答え (3)
(b) 図1の回路に図2の回路を接続したときに回路に流れる電流を $I$ [A] とすると、
$I=\displaystyle\frac{E_o}{R_m+R_s+R_o}=\displaystyle\frac{5}{23+4977+50}=0.99×10^{-3}[A]$
したがって、電圧 $V_p$ [V] は、
$V_p=E_o-IR_o=5-0.99×10^{-3}×50=4.95$ [V]
答え (2)
2004年(平成16年)問13
内部抵抗 r=2 [kΩ] 、最大目盛 1 [V] の直流電圧計がある。この電圧計に Rm1=18 [kΩ]、Rm2=40 [kΩ] の抵抗を図のように接続して、測定範囲を拡大した。
図の端子C,D(負極端子)を用いて直流電圧源の電圧 8 [V] を測定したとき、電圧計の指針の振れを示す図として最も近いのは次のうちどれか。
ただし、直流電圧源の内部抵抗は無視できるものとする。また、電圧計の目盛は等分目盛とする。
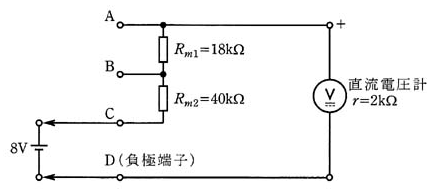
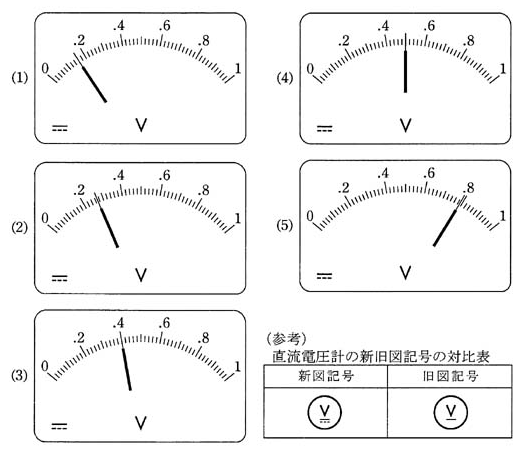
2004年(平成16年)問13 過去問解説
直流電圧 8 [V] を加えたときに、電圧計に流れる電流を $I$ [A]とすると、
$I=\displaystyle\frac{8}{R_{m1}+R_{m2}+r}=\displaystyle\frac{8}{(18+40+2)×10^3}=1.33×10^{-4}[A]$
内部抵抗 $r$ に加わる電圧 $V$ は、
$V=I×r=1.33×10^{-4}×2×10^{3}=0.266$[V]
答え (2)
2007年(平成19年)問14
次の文章は、電圧計と電流計を用いて抵抗負荷の直流電力を測定する場合について述べたものである。
電源 E [V] 、負荷抵抗 R [Ω] 、内部抵抗 Rv [Ω] の電圧計及び内部抵抗 Ra[Ω]の電流計をそれぞれ図1、図2のように結線した。図1の電圧計及び電流計の指示値はそれぞれ V1 [V] 、I1 [A] 、図2の電圧計及び電流計の指示値はそれぞれ V2 [V] 、I2 [A] であった。
図1の回路では、測定で求めた電力 V1I1 [W] には、計器の電力損失( ア ) [W] が誤差として含まれ、図2の回路では、測定で求めた電力電力 V2I2 [W] には、同様に( イ ) [W] が 誤差として含まれる。
したがって、Rv= 10〔kΩ〕、Ra= 2 [Ω] 、 R= 160 [Ω] であるときは、( ウ )の回路を利用する方が、電力測定の誤差率を小さくできる。
ただし、計器の電力損失に対する補正は行わないものとする。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまるる語句文は式とし、正しいものを組合せたのは次のうちどれか。
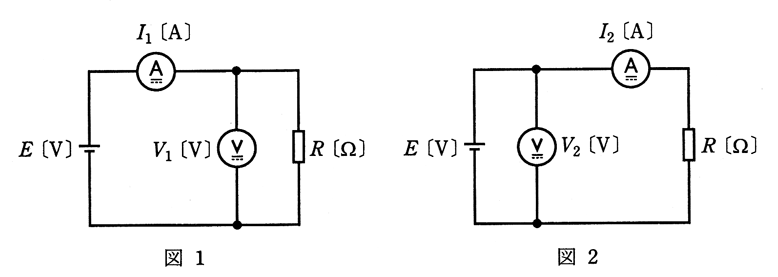
| (ア) | (イ) | (ウ) | |
| (1) | $\displaystyle\frac{V_1^2}{R_v}$ | $I_2^2R_a$ | 図2 |
| (2) | $I_1^2R_a$ | $\displaystyle\frac{V_2^2}{R_v}$ | 図1 |
| (3) | $I_1^2R_a$ | $\displaystyle\frac{V_2^2}{R_v}$ | 図2 |
| (4) | $\displaystyle\frac{V_1^2}{R_v}$ | $I_2^2R_a$ | 図1 |
| (5) | $I_1^2R_a$ | $\displaystyle\frac{V_2^2}{R_v}$ | 図2 |
2007年(平成19年)問14 過去問解説
図1では、電流 $I_1$ は、電圧計の内部抵抗 $R_v$ と負荷抵抗 $R$ に流れる電流の和になりますので、測定電力 $V_1I_1$ [W] は、
$V_1I_1=\displaystyle\frac{V_1^2}{R_v}+\displaystyle\frac{V_1^2}{R}[W]$
なので、計器の電力損失(ア)は $\displaystyle\frac{V_1^2}{R_v}$ になります。
図2では、電圧 $V_2$ は、電流計の内部抵抗 $R_a$ と負荷抵抗 $R$ に加わる電圧の和になりますので、測定電力 $V_2I_2$ [W] は、
$V_2I_2=(I_2R+I_2R_a)I_2=I_2^2R+I_2^2R_a$ [W]
なので、計器の電力損失(イ)は $I_2^2R_a$ になります。
図1の誤差率 $ε_1$ および図2の誤差率 $ε_2$は、
$ε_1=\displaystyle\frac{\displaystyle\frac{V_1^2}{R_v}}{\displaystyle\frac{V_1^2}{R}}×100=\displaystyle\frac{160}{10000}×100=1.6[%]$
$ε_2=\displaystyle\frac{I_2^2R_a}{I_2^2R}×100=\displaystyle\frac{2}{160}×100=1.25[%]$
( 図2 )の回路を利用する方が、電力測定の誤差率を小さくできます。
答え (1)
2007年(平成19年)問16
可動コイル形計器について、次の(a)及び(b)に答えよ。
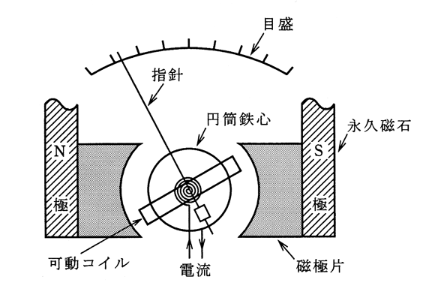
(a) 次の文章は、可動コイル形電流計の原理について述べたもので、図はその構造を示す原理図である。
計器の指針に働く電流によるトルクは、その電流の( ア )に比例する。これに脈流を流すと可動部の( イ )モーメントが大きいので、指針は電流の( ウ )を指示する。
この計器を電圧計として使用する場合、( エ )を使う。
上記の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる語句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 1乗 | 慣性 | 平均値 | 倍率器 |
| (2) | 1乗 | 回転 | 平均値 | 分流器 |
| (3) | 1乗 | 回転 | 瞬時値 | 倍率器 |
| (4) | 2乗 | 回転 | 実効値 | 分流器 |
| (5) | 2乗 | 慣性 | 実効値 | 倍率器 |
(b) 内部抵抗 $r_a=2$ [Ω]、細大目盛 $I_m=10$ [mA]の可動コイル形電流計を用いて、最大 150 [mA]と最大 1 [A]の直流電流を測定できる多重範囲の電流計を作りたい。そこで、図のような二つのー端子を有する多重範囲の電流計を考えた。抵抗 $R_1$ [Ω],$R_2$ [Ω]の値として、最も近いものを組み合わせたのは次のうちどれか。
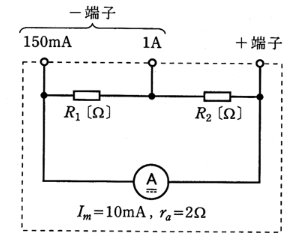
$R_1$ [Ω] $R_2$ [Ω]
(1)0.12 0.021
(2)0.12 0.042
(3)0.14 0.021
(4)0.24 0.012
(5)0.24 0.042
2007年(平成19年)問16 過去問解説
(a) 次の文章は、可動コイル形電流計の原理について述べたもので、図はその構造を示す原理図である。
計器の指針に働く電流によるトルクは、その電流の( 1乗 )に比例する。これに脈流を流すと可動部の( 慣性 )モーメントが大きいので、指針は電流の( 平均値 )を指示する。
この計器を電圧計として使用する場合、( 倍率器 )を使う。
答え (1)
(b) 図1は最大 150mA 測定する場合の、図2は最大 1A 測定する場合場合の等価回路です。
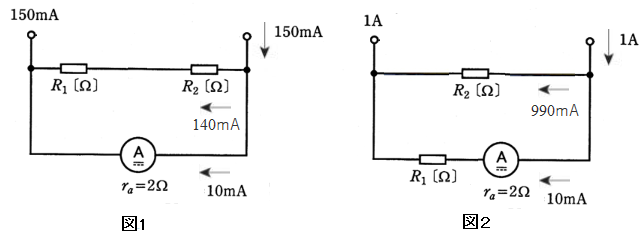
図1より
$140×10^{-3}×(R_1+R_2)=10×10^{-3}×2$ … (1)
図2より
$990×10^{-3}×R_2=10×10^{-3}×(R_2+2)$ … (2)
式(1),(2)を解くと
$R_1=0.12$,$R_2=0.021$
答え (1)
2010年(平成22年)問14
次の文章は、直流電流計の測定範囲拡大について述べてものである。
内部抵抗 $r =10$ [mΩ] 、最大目盛 0.5 [A] の直流電流計Mがある。この電流計と抵抗 $R_1$ [mΩ] 及び $R_2$ [mΩ] を図のように結線し、最大目盛が 1 [A] と 3 [A] からなる多重範囲電流計を作った。この多重範囲電流計において、端子3Aと端子+を使用する場合、抵抗( ア ) [mΩ] が分流器となる。端子 1A と端子+を使用する場合には、抵抗( イ ) [mΩ] が倍率( ウ )倍の分流器となる。また、3 [A] を最大目盛とする多重範囲電流計の内部抵抗は( エ ) [mΩ] となる。
上記の記述中の空白個所(ア),(イ),(ウ)及び(エ)に当てはまる式又は数値として、正しいものを組み合わせたのは次のうちどれか。
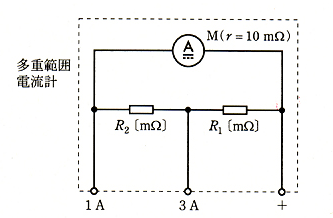
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | $R_2$ | $R_1$ | $\displaystyle\frac{10+R_2}{R_1}+1$ | $\displaystyle\frac{20}{3}$ |
| (2) | $R_1$ | $R_1+R_2$ | $\displaystyle\frac{10+R_2}{R_1}$ | $\displaystyle\frac{25}{9}$ |
| (3) | $R_2$ | $R_1+R_2$ | $\displaystyle\frac{10}{R_1+R_2}+1$ | $5$ |
| (4) | $R_1$ | $R_2$ | $\displaystyle\frac{10}{R_1+R_2}$ | $\displaystyle\frac{10}{3}$ |
| (5) | $R_1$ | $R_1+R_2$ | $\displaystyle\frac{10}{R_1+R_2}+1$ | $\displaystyle\frac{25}{9}$ |
2010年(平成22年)問14 過去問解説
図1は最大 3A を測定する場合の、図2は最大 1A 測定する場合場合の等価回路です。
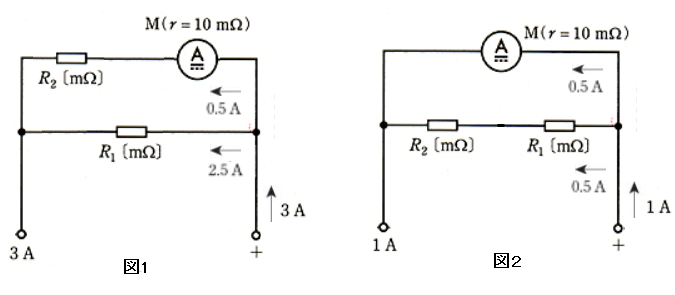
図1の回路では、抵抗 $R_1$ (ア) [mΩ] が分流器となります。
この多重範囲電流計において、端子3Aと端子+を使用する場合、抵抗( $R_1$ ) [mΩ] が分流器となる。端子1Aと端子+を使用する場合には、抵抗( $R_1+R_2$ ) [mΩ] が倍率( $\displaystyle\frac{10}{R_1+R_2}+1$ )倍の分流器となる。
図1より
$0.5(R_2+10×10^{-3})=2.5R_1$
$5R_1-R_2=10×10^{-3}$ … (1)
図2より
$0.5×10×10^{-3}=0.5(R_1+R_2)$
$R_1+R_2=10×10^{-3}$ … (2)
式(1),(2)を解くと
$R_1=\displaystyle\frac{10×10^{-3}}{3}$,$R_2=\displaystyle\frac{20×10^{-3}}{3}$
3 [A] を最大目盛とする多重範囲電流計の内部抵抗( エ ) [mΩ] は、
$\displaystyle\frac{\displaystyle\frac{10}{3}\left(\displaystyle\frac{20}{3}+10\right)}{\displaystyle\frac{10}{3}+\left(\displaystyle\frac{20}{3}+10\right)}=\displaystyle\frac{25}{9} [mΩ] $
答え (5)
2012年(平成24年)問17
直流電圧計について、次の(a)及び(b)の問に答えよ。
(a) 最大目盛 1 [V]、内部抵抗 rv=1000 [Ω] の電圧計がある。この電圧計を用いて最大目盛 15 [V] の電圧計とするための、倍率器の抵抗 Rm [kΩ] の値として、正しいものを次の(1)~(5)のうちから一つ選べ。
(1) 12 (2) 13 (3) 14 (4) 15 (5) 16
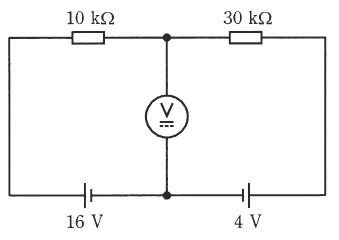
(b) 図のような回路で上記の最大目盛 15 [V] の電圧計を接続して電圧を測ったときに、電圧計の指示 [V] はいくらになるか。最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 7.2 (2) 8.7 (3) 9.4 (4) 11.3 (5) 13.1
2012年(平成24年)問17 過去問解説
(a) 問を図で示します。
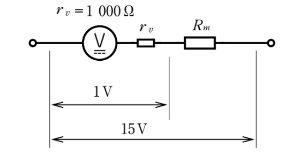
$1=\displaystyle\frac{1×10^3}{R_m+1×10^3}×15$
$R_m+1×10^3=15×10^3$
$R_m=14×10^3$
答え (3)
(b) キルヒホッフの法則で解きます。
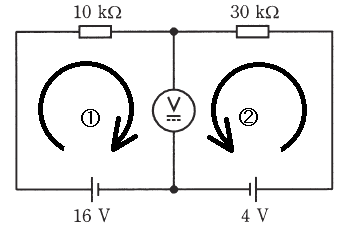
①の回路
$10I_1+15(I_1+I_2)=16$
$25I_1+15I_2=16$ … (1)
②の回路
$30I_2+15(I_1+I_2)=4$
$15I_1+45I_2=4$ … (2)
式(1),(2)を解くと
$I_1=0.733$[mA],$I_2=-0.155$[mA]
問(a)の条件より、電圧計の部分は15 [kΩ] の抵抗と見ることができますので、求める電圧 $V$ は、
$V=(0.733-0.155)×10^{-3}×15×10^3=8.67$[V]
答え (2)
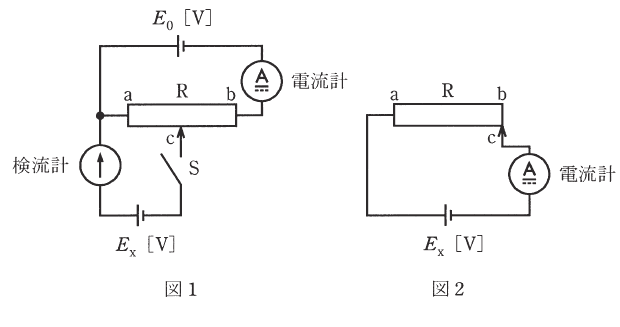
2015年(平成27年)問15
図のように、a-b間の長さが 15cm、最大値が 30Ω のすべり抵抗器R、電流計、検流計、電池 E0 [V] 、電池 Ex [V] が接続された回路がある。この回路において次のような実験を行った。
実験Ⅰ:図1でスイッチSを開いたとき、電流計は 200mA を示した。
実験Ⅱ:図1でスイッチSを閉じ、すべり抵抗器 R の端子cをbの方向へ移動させて行き、検流計が零を指したとき移動を停止した。このときa-c間の距離は 4.5cm であった。
実験Ⅲ:図2に配線を変更したら、電流計の値は 50mA であった。
次の(a)及び(b)の問に答えよ。ただし、各計測器の内部抵抗及び接触抵抗は無視できるものとし、また、すべり抵抗器Rの長さ [cm] と抵抗値 [Ω] とは比例するものであるとする。
(a) 電池 Ex の起電力の値 [V] として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 1.0 (2) 1.2 (3) 1.5 (4) 1.8 (5) 2.0
(b) 電池 Ex の内部抵抗の値 [Ω] として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.5 (2) 2.0 (3) 3.5 (4) 4.2 (5) 6.0
2015年(平成27年)問15 過去問解説
(a) 実験Ⅰより、すべり抵抗の両端の電圧は、
$200mA×30Ω=6V$
実験Ⅱより、抵抗と長さは比例しますので、a-c間の電圧は、
$\displaystyle\frac{4.5cm}{15cm}×6V=1.8V$
となります。図1の等価回路を示します。
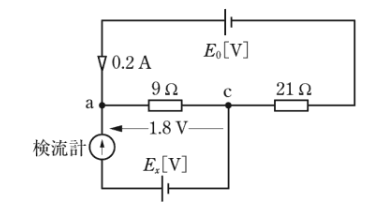
等価回路図より、電池Exの起電力の値 [V] は、1.8V となります。
答え (4)
(b) 実験3より、図2の等価回路を示します。
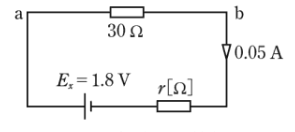
$1.8=0.05(30+r)$
$r=6$ [Ω]
答え (5)



