これだけは知っておきたい電気設備の基礎知識をご紹介します。このページでは「電力の測定方法」について、維持管理や保全などを行う電気技術者の方が、知っておくとためになる電気の基礎知識を解説しています。
単相電力の測定
消費電力 $P$〔W〕、力率 $cosθ$ の負荷に交流電圧を加え、交流電圧計(V)、交流電流計(A)および単相電力計(W) を第1図のように接続した単相交流回路があります。この場合、電圧計の指示 $V$〔V〕と電流計の指示 $I$〔A〕{(V)、(A)は交流電圧、電流計であるから実効値を指示する} を掛けた、$VI$ は皮相電力〔VA〕を表わし、負荷 の有効電力 $P$ は $P=\sqrt{3}VIcosθ$ ですので、負荷力率 $cosθ$ がわからないと電力は測定できなません。
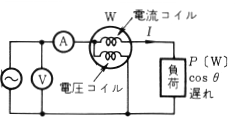
単相電力計は図に示すように、電圧コイルと電流コイルを有し、それぞれのコイルに流れる電流の内積、つまり $ VIcosθ$ に比例したトルクを生じるようになっています。したがって電力計の指示 $W$ は、
$W=VIcosθ=P$〔W〕
となり、有効電力を指示します。
三相電力の測定
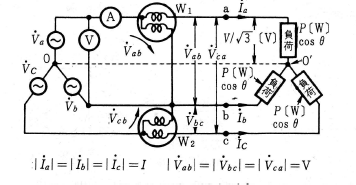
対称三相交流電源に、三相平衡負荷を接続した、第2図に示すような平衡三相交流回路があり、これに、交流電圧計(V)、交流電流計(A) が接続してあります。図より、(V)、(A)は線間電圧、線電流を測定しており、その指示をそれぞれ $V$〔V〕、$I$〔A〕とします。平衡三相回路ですので、点線で示した中性線を仮想すると、三相回路は、三つの単相交流回路に分けて考えることができます。
a相 だけを考えれば、第3図のようになり、線間電圧が $V$〔V〕ですので、a相の相電圧は、
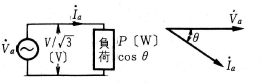
$|\dot{V}_a|=\displaystyle \frac{V}{\sqrt{3}}$
したがってa相の有効電力 $P_a$ は、
$P_a=|\dot{V}_a||\dot{I}_a|cosθ=\displaystyle \frac{V}{\sqrt{3}}Icosθ=P$〔W〕
となります。また、他のb相、c相についても負荷が同じであるので、三相電力は一相の電力の 3倍となり、
$3P_a=3|\dot{V}_a||\dot{I}_a|cosθ=3\displaystyle \frac{V}{\sqrt{3}}Icosθ=3P$〔W〕
で表わすことができ、平衡三相交流回路の電力は、
$\sqrt{3}$×(線間電圧)×(線電流)×(一相の負荷力率)
で求めることができます。同様に
三相皮相電力$=\sqrt{3}VI$〔VA〕
三相無効電力$=\sqrt{3}VIsinθ$〔var〕
で求めることができます。(この式は、Y結線 、△結線にかかわらず、成り立つ式である)。負荷が不平衡の場合 は、線電流が異なってくるので、三相電力を $\sqrt{3}VIcosθ$ では求めることはできず、計算は複雑になります。
三相電力測定におけるプロンデルの定理
ブロンデルの定理とは、多相交流において(n-1) 個の単相電力計があれば、電力を測定できるというものです。三相交流の場合は2個の単相電力計があれば、 三相電力を測定することができ、負荷の平衡、不平衡にかかわらず成り立つ定理です。
次にこれを証明してみます。2個の単相電力計を第2図に示すように接続し、その場合の各電力計の指示を、それぞれ $W_1$〔W〕、$W_2$〔W〕とします。三相交流電源の相回転を a,b,c とするとベクトル図は第4図のようになります。このベクトル図より各電力計の指示を求めると、
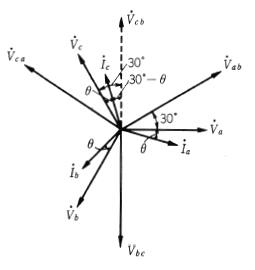
$W_1=$(電圧コイルに加わる電圧と電流コイルに流れる電流の内積)
$W_1=\dot{V}_{ab}×\dot{I}_{a} =VIcos(30+θ)$〔W〕
$W_2=\dot{V}_{cb}×\dot{I}_{c}=VIcos(30-θ)$〔W〕
(電圧コイルには $\dot{V}_{cb}$ の電圧が加わり、$\dot{V}_{cb}$ は $\dot{V}_{bc}$ と反対位相)
ここで $W_1+W_1$ を求めると、
$W_1+W_1=VI {cos(30+θ)+cos(30-θ)}=\sqrt{3}VI cosθ$〔W〕
となり、2つの電力計の読みの和、 $W_1+W_1$ は三相回路の電力を表わしています。
同様に $W_1-W_1$ は $\sqrt{3}VI sinθ$ となり、三相無効電力を表わします。三相電力計は、このブロンデルの定理を応用したもので、内部に 2個の単相電力計の要素を内蔵した構造をしており、この和が指示に表われるようになっています。
受変電設備の電カ・電力量・力率
第5図のように、三相3線式 6600〔V〕で受電し、これを変圧器で三相3線式 220〔V〕に降圧して、2組の三相平衡負荷に電力を供給している受変電設備があります。この場合の交流電流計、電力計、力率計の指示を求めてみます。
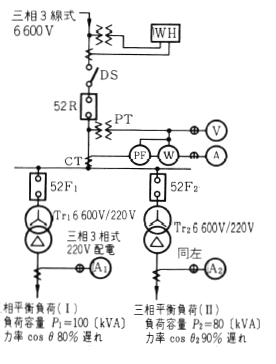
〔負荷Ⅰ〕
皮相電力$=P_1=100$〔 kVA〕
有効電力$=P_1cosθ_1=100×0.8=80$〔kW〕
無効電力$=P_1sinθ_1=100×\sqrt{1-(0.8)^2}=60$〔kVar〕
〔負荷Ⅱ〕
皮相電力$=P_2=80$〔kVA〕
有効電力$=P_2cosθ_2=80×0.9=72$〔kW〕
無効電力$=P_2sinθ_2=80×\sqrt{1-(0.9)^2}=34.9$〔kVar〕
これをベクトル図に示すと第6図 (a)(b)のようになります。
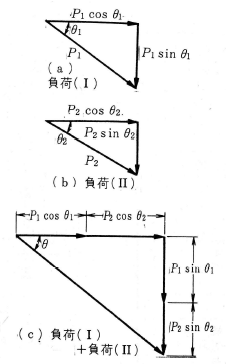
次に、二つの負荷を合成してみます。二つ以上の負荷を合成する場合は、次のようにします。
合成有効電力=おのおのの負荷の有効電力の和
合成無効電力=おのおのの負荷の無効電力の和
合成皮相電力
(1)力率が同一の場合
合成皮相電力=おのおのの皮相電力の和
(2)力率が異なる場合
合成皮相電力$=\sqrt{(合成有効電力)^2+(合成無効電カ)^2}$
皮相電力は力率が異なる場合は、それぞれの負荷の皮相電力の和とはならず、ベクトル的に合成しなければなりませんので、注意が必要です。このことは、皮相電流についても同 じことがいえます。
この場合は、第6図 (c)のベクトル図より
合成有効電力$=P_1cosθ_1+P_2cosθ_2=80+72=152$〔kW〕
合成無効電力$=P_1sinθ_1+P_2sinθ_2=60+34.9=94.9$〔kVar〕
合成皮相電力$=\sqrt{152^2+94.9^2}=179$〔 kVA〕
合成力率$=\displaystyle \frac{152}{179}≒0.85$
したがって、電力計の指示は 152〔kW〕、力率計の指示は 85% となります。
次に電流計の指示を求めてみます。負荷 Ⅰ,Ⅱの電流を $I_1,I_2$ とし、 Tr 二次回路線間電圧を $V$〔V〕とすれば、
$I_1=\displaystyle \frac{P_1}{\sqrt{3}V}=\displaystyle \frac{100×10^3}{\sqrt{3}×220V}≒262$〔A〕
(皮相電力$=\sqrt{3}$×線間雪圧×線電流より)
$I_2=\displaystyle \frac{P_2}{\sqrt{3}V}=\displaystyle \frac{80×10^3}{\sqrt{3}×220V}≒210$〔A〕
となり、$I_1,I_2$ は皮相電流 (線電流)を表わしています。また、皮相 ,有効 ,無効電力を $\sqrt{3}V$ で割った ものは、それぞれの負荷あるいは合成負荷の一相の皮相, 有効 ,無効電流を表わしており、ベクトル図も同じで、ただベクトルの大きさが $\displaystyle \frac{1}{\sqrt{3}V}$ になっただけになります。
したがって、合成電流を求める場合、それぞれの負荷の有効 ,無効電流を求め、ベクトル的に合成するか、合成皮相電力から求めるかの、二つの方法があります。この場合、合成皮相電力から求めると、合成電流 $I$ は、
$I=\displaystyle \frac{179×10^3}{\sqrt{3}V}≒ 470$〔A〕
となり、変圧器の変圧比が 6600/220 であるから、Tr一次側の電流は、
$\displaystyle \frac{470×220}{6600}≒15.7$〔A〕
となります。 したがって、電流計の指示はそれぞれ 15.7〔 A〕,262〔A〕 , 210〔A〕を指示します。なお、負荷 I を24時間使用、負荷Ⅱ を8時間から18時の間使用した場合の、取引用電力量計 WHの 1日間の計量値、つまり 1日当たりの電力使用量は、
{80〔kW〕×24〔時間〕}+ {72〔kW〕×10〔時間〕}=2640〔kWh〕
となります。



