三相誘導電動機の特性

このページでは、三相誘導電動機の特性について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の機械科目で、実際に出題された三相誘導電動機の特性の過去問題の解き方も解説しています。

三相誘導電動機の速度特性

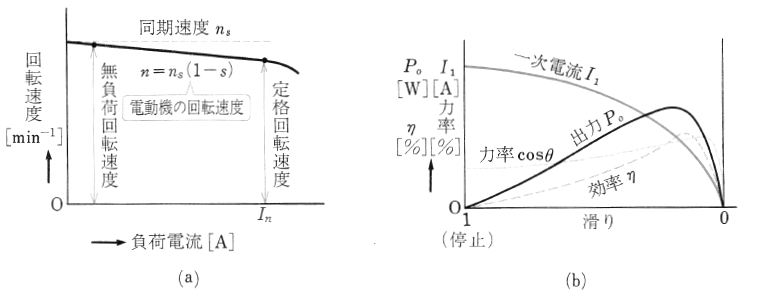
三相誘導電動機の回転速度は、図1(a)に示すように、負荷によって変化しますが、無負荷時と全負荷時との回転速度の差は非常に小さいので、三相誘導電動機は直流分巻電動機と同じように「定速度電動機」となります。

また、回転速度が変わり、滑りが変わると、二次電流 $I_2$［A］、一次電流 $I_1$［A］、出力 $P_o$［W］、効率 $η$［%］なども変化します。図1(b)は、一次電圧を一定に保ち、回転速度 $n$［min^-1］のかわりに滑り $s$ をとり、滑り $s$ に対する一次電流 $I_1$［A］、出力 $P_o$［W］、力率 $cosθ$、効率 $η$［%］の変化のようすを示したもので、これを「速度特性曲線」といいます。

三相誘導電動機のトルク特性

電動機のトルクが $T$［N･m］、角速度が $ω$［rad/s］、回転速度が $n$［min^-1］とすれば、出力 $P_o$［W］は次の式で表すことができます。

$P_o=ωT=2π\displaystyle\frac{n}{60}T$ … (1)

$T=\displaystyle\frac{60}{2π}・\displaystyle\frac{P_o}{n}$ … (2)

式(1)に、$P_o=P_2(1-s)$ および $n=n_s(1-s)$ を代入すると、二次入力 $P_2$［W］は、次の式で表すことができます。

$P_2=2π\displaystyle\frac{n_s}{60}T$ … (3)

式(1)で示す出力は、トルク $T$［N･m］を発生して回転速度 $n$［min^-1］で回転しているときの電力を表しています。これに対して、式(3)の二次入力 $P_2$［W］は、同じトルクのもとで、同期速度で回転しているときの出力電力を表しています。これを同期ワットといいます。 誘導電動機のトルク $T$［N･m］は、同期ワット $P_2$［W］に比例しているので、トルクを表すとき、出力 $P_o$［W］のかわりに、$P_2$［W］つまり同期ワットで表すことが多いです。

滑りとトルクの関係

式(3)から、トルク $T$［N･m］は、次の式で表すことができます。

$T=\displaystyle\frac{60}{2πn_s}P_2=KP_2$ … (4)

また、式(4)に一次負荷電流と二次入力の式を代入すると、式(5)が得られます。

$T=3K\displaystyle\frac{{V_1}^2\displaystyle\frac{{r_2}’}{s}}{\left(r_1+\displaystyle\frac{{r_2}’}{s}\right)^2+(x_1+{x_2}’)^2 }$ … (5)

式(5)において、${r_1}$，${r_2}’$，$x$，${x_2}’$ は定数ですから、誘導電動機のトルク $T$［N･m］は、滑り $s$ が一定であれば、一次電圧 $V_1$［V］の2乗に比例します。

また、一定電圧で運転中に負荷の影響を受けるのは滑り $s$ であることがわかります。滑り $s$ とトルク $T$［N･m］の関係は図2に示す曲線になります。これをトルク-速度曲線といいます。

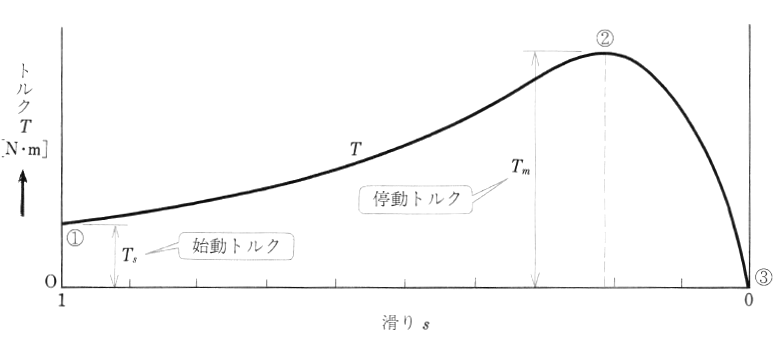
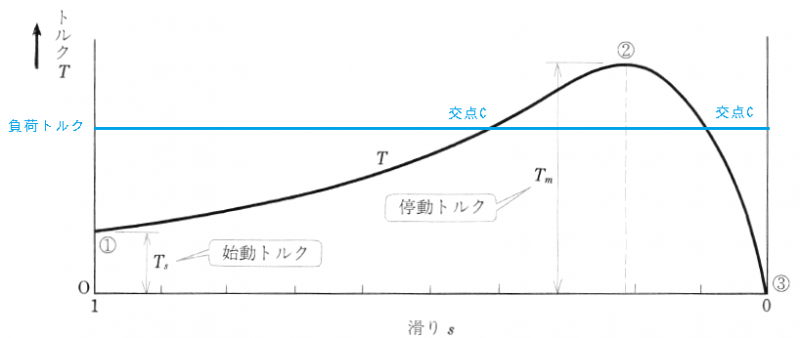
図2において、$s=1$ のときのトルク $T_s$［N･m］は、「始動トルク」とよばれ、式(5)から $T_s= 3K\displaystyle\frac{{V_1}^2{r_2}’}{(r_1+{r_2}’)^2+(x_1+{x_2}’)^2 }$ で、表わすことができます。始動トルク $T_s$［N･m］は図2の点①に示される小さな値です。点①から最大トルク $T_m$［N･m］を生じる点②までは、トルク $T$［N･m］は、滑り $s$ にほぼ反比例して増加し、点②を過ぎると滑り $s$ にほぼ比例して減少し、$s=0$ の点③では、トルクは $0$ になります。なお、最大トルク $T_m$［N･m］は、「停動トルク」ともよばれています。

比例推移

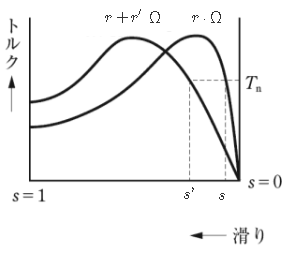
式(5)において、$V_1$［V］，$r_1$［Ω］，$x_1$［Ω］，${x_2}’$［Ω］が、一定で、$\displaystyle\frac{{r_2}’}{s}$［Ω］の値が変わらなければ、$T$［N･m］の値も変わりません。図3において二次巻線抵抗 ${r_2}’$［Ω］を 2倍にすれば、$s$ が 2倍になり、${r_2}’$［Ω］を 3倍にすれば、$s$ は 3倍になることを意味します。これは、二次回路の抵抗 ${r_2}’$［Ω］、外部抵抗 $R_s$［Ω］の和の値が、もとの抵抗 ${r_2}’$［Ω］の m倍になれば、そのときの滑り $s_2$ は、もとの滑り $s_1$ の m倍になります。この関係は次の式で表すことができます。

$\displaystyle\frac{{r_2}’}{s_1}=\displaystyle\frac{m{r_2}’}{ms_1}=\displaystyle\frac{{r_2}’+R_s}{s_2}$ … (6)

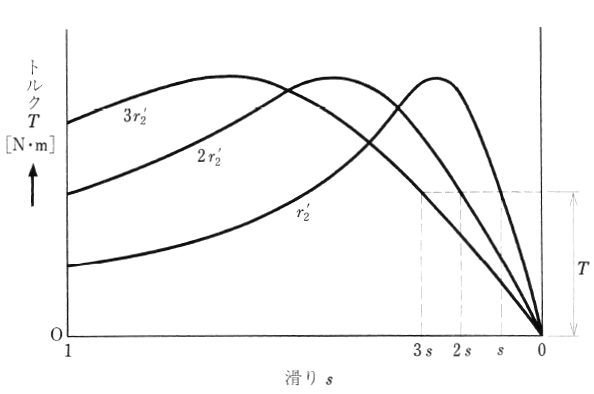
図3は、${r_2}’$［Ω］の値によって、 トルク-速度曲線がどのように変化するかを示したものです。${r_2}’$ が大きくなると、この曲線は滑り $s$ の大きいほうへ移動します。トルク $T$ が一定なら、$s$ の値はつねに ${r_2}’$ に比例して推移しますので、この曲線の推移のしかたを「比例推移」といいます。この性質を利用すると、${r_2}’$ に適切な値を選ぶことによって、始動時に最大トルクを得ることができ、始動特性を改善することができます。

なお、電流・力率などもトルクと同様に、二次回路の抵抗 ${r_2}’$ の大きさに従って比例推移します。

　　

電験三種－機械（誘導機）過去問

1998年（平成10年）問13

定格周波数 50［Hz］、4極の三相誘導電動機があり、トルク 100［N･m］の負荷を負って 1440［r/min］で運転している。負荷トルクを 50［N･m］に変更したときの電動機出力［kW］の値として、正しいのは次のうちどれか。ただし、電動機の滑りとトルクは比例するものとする。

(1) 7.5　(2) 7.7　(3) 7.9　(4) 74　(5) 79

1998年（平成10年）問13　過去問解説

同期速度を $n_s$［min^-1］とすると、

$n_s=\displaystyle\frac{120f}{p}=\displaystyle\frac{120×50}{4}=1500$［min^-1］

回転速度を $n$［min^-1］とすると、すべり $s$ は、

$s=\displaystyle\frac{n_s-n}{n_s}=\displaystyle\frac{1500-1440}{1500}=0.04$

負荷トルクを 50［N･m］に変更したときのすべりを $s’$ とすると、題意よりすべりはトルクに比例しますので、

$s:s’=100:50$
$0.04:s’=100:50$
$s’=0.02$

負荷トルクを 50［N･m］に変更したときの電動機出力 $P’$［kW］は、

$P’=ω’T’=2π\displaystyle\frac{n’}{60}T’=2π\displaystyle\frac{n_s(1-s’)}{60}T’$

　$=2π\displaystyle\frac{1500(1-0.02)}{60}×50=7.7$［kW］

答え (2)

2000年（平成12年）問12

定格周波数 60［Hz］、6極の三相巻線形誘導電動機があり、二次巻線を短絡して定格負荷で運転したときの回転速度は1,170［r/min］である。この電動機について、次の(a)及び(b)に答えよ。
ただし、電動機の二次抵抗値が一定のとき、滑りとトルクは比例関係にあるものとする。

(a) この電動機を定格負荷の 80［%］のトルクで運転する場合、二次巻線が短絡してあるときの滑り［%］の値として、正しいのは次のうちどれか。

(1) 1.5　(2) 2　(3) 2.5　(4) 3　(5) 4

(b) この電動機を定格負荷の 80［%］のトルクで運転する場合、二次巻線端子に三相抵抗器を接続し、二次巻線回路の1回路当たりの抵抗値を短絡時の 2.5 倍にしたときの回転速度［r/min］の値として、正しいのは次のうちどれか。

(1) 980　(2) 1110　(3) 1140　(4) 1170　(5) 1200

2000年（平成12年）問12　過去問解説

(a) 同期速度を $n_s$［min^-1］とすると、

$n_s=\displaystyle\frac{120f}{p}=\displaystyle\frac{120×60}{6}=1200$［min^-1］

回転速度を $n$［min^-1］とすると、すべり $s$ は、

$s=\displaystyle\frac{n_s-n}{n_s}=\displaystyle\frac{1200-1170}{1200}=0.025$

定格負荷の 80［%］のトルクで運転する場合のすべりを $s’$ とすると、題意よりすべりはトルクに比例しますので、

$s:s’=100:80$
$0.025:s’=10:8$
$s’=0.02=2$［%］

答え (2)

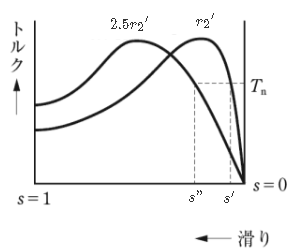
(b) 二次巻線が短絡してあるときの抵抗を ${r_2}’$［Ω］とすると、二次巻線回路の１回路当たりの抵抗値を短絡時の 2.5倍にしたときのすべり $s”$ は、抵抗と比例推移しますので、

$\displaystyle\frac{{r_2}’}{s’}=\displaystyle\frac{2.5{r_2}’}{ s” }$

$\displaystyle\frac{1}{0.02}=\displaystyle\frac{2.5}{ s” }$

$s”=0.05$

そのときの回転速度 $n”$［min^-1］は、

$s’’=\displaystyle\frac{n_s-n’’}{n_s}$

$0.05=\displaystyle\frac{1200-n’’}{1200}$

$n”=1200×(1-0.05)=1140$［min^-1］

答え (3)

2004年（平成16年）問4

定格出力 36［kW］、定格周波数 60［Hz］、8極のかご形三相誘導電動機があり、滑り 4［%］で定格運転している。このとき、電動機トルク［N･m］の値として、最も近いのは次のうちどれか。

(1) 382　(2) 398　(3) 428　(4) 458　(5) 478

2004年（平成16年）問4　過去問解説

同期速度を $n_s$［min^-1］とすると、

$n_s=\displaystyle\frac{120f}{p}=\displaystyle\frac{120×60}{8}=900$［min^-1］

回転速度を $n$［min^-1］とすると、すべりは $s$ は 4［%］ですので、

$s=\displaystyle\frac{n_s-n}{n_s}$

$0.04=\displaystyle\frac{900-n}{900}$

$n=900×(1-0.04)=864$［min^-1］

電動機のトルクを $T$［N･m］、角速度を $ω$［rad/s］、出力を $P_o$［W］とすれば、

$P_o=ωT=2π\displaystyle\frac{n}{60}T$

$36000=2π\displaystyle\frac{864}{60}T$

$T=36000×\displaystyle\frac{60}{2π×864}=398$［N･m］

答え (2)

2005年（平成17年）問15

三相誘導電動機について、次の(a)及び(b)に答えよ。

(a) 一次側に換算した二次巻線の抵抗 ${r_2}’$ と滑り $s$ の比 ${r_2}’$/$s$ が、他の定数(一次巻線の抵抗 ${r_1}$ 、一次巻線のリアクタンス ${x_1}$ 、一次側に換算した二次巻線のリアクタンス ${x_2}’$ )に比べて十分に大きくなるように設計された誘導電動機がある。この電動機を電圧 $V$ の電源に接続して運転したとき、この電動機のトルク $T$ と滑り $s$ 、電圧 $V$ の関係を表す近似式として、正しいのは次のうちどれか。ただし、$k$ は定数である。

(1) $T=kV^2s$　(2) $T=kVs$　(3) $T=\displaystyle\frac{kV^2}{s}$　(4) $T=\displaystyle\frac{k}{Vs}$　(5) $T=\displaystyle\frac{k}{V^2s}$

(b) 上記(a)で示された条件で設計された定格電圧 220［V］、同期速度 1200［min^-1］の三相誘導電動機がある。この電動機を電圧 220［V］の電源に接続して、一定トルクの負荷で運転すると、1140［min^-1］の回転速度で回転する。この電動機に供給する電源電圧を 200［V］に下げたときの電動機の回転速度［min^-1］の値として、最も近いのは次のうちどれか。
ただし、電源電圧を下げたとき、負荷トルクと二次抵抗の変化はしないものとする。

(1) 1000　(2) 1091　(3) 1113　(4) 1127　(5) 1150

2005年（平成17年）問15　過去問解説

(a) 回転子巻線(二次巻線)の1相分の二次電流 $I_2$［A］は、

$I_2=\displaystyle\frac{E_2}{\sqrt{\left(\displaystyle\frac{{r_2}’}{s}\right)^2+{{x_2}’}^2}}=\displaystyle\frac{\displaystyle\frac{V}{\sqrt{3}}}{\sqrt{\left(\displaystyle\frac{{r_2}’}{s}\right)^2+{{x_2}’}^2}}$

1相分の二次入力を ${P_2}’$［W］とすると、

${P_2}’={I_2}^2\displaystyle\frac{{r_2}’}{s}$

3相分の二次入力を ${P_2}$［W］は、$3{P_2}’$［W］となります。トルクを $T$［N･m］、角速度を $ω$［rad/s］とすれば、 ${P_2}$［W］との関係は、

${P_2}=ωT=2π\displaystyle\frac{n}{60}T$

$T=\displaystyle\frac{60}{2πn}×{P_2}=\displaystyle\frac{60}{2πn}×3{I_2}^2\displaystyle\frac{{r_2}’}{s}$

　$=\displaystyle\frac{90}{πn}×\displaystyle\frac{(\displaystyle\frac{V}{\sqrt{3}})^2}{\left(\displaystyle\frac{{r_2}’}{s}\right)^2+{{x_2}’}^2}×\displaystyle\frac{{r_2}’}{s}$

題意より ${r_2}’>> {x_2}’$ ですので、${x_2}’$ を無視すると、

$T=\displaystyle\frac{30}{πn}×\displaystyle\frac{V^2}{\left(\displaystyle\frac{{r_2}’}{s}\right)^2}×\displaystyle\frac{{r_2}’}{s}$

　$=\displaystyle\frac{30}{πn{r_2}’}×V^2s=kV^2s$

答え (1)

(b) 定格電圧 220［V］のときのすべりを $s_1$ 、回転速度を $n_1$［min^-1］とすると、

$s_1=\displaystyle\frac{n_s-n_1}{n_s}=\displaystyle\frac{1200-1140}{1200}=0.05$

電源電圧を 200［V］に下げたときのすべりを $s_2$、回転速度を $n_2$［min^-1］とすると、$T=kV^2s$ よりトルクは一定なので、$s_2$ は $V^2$ に反比例することになります。したがって、

$s_2=s_1×\left(\displaystyle\frac{220}{200}\right)^2=0.05×\left(\displaystyle\frac{220}{200}\right)^2=0.0605$

$s_2=\displaystyle\frac{n_s-n_2}{n_s}$

$0.0605=\displaystyle\frac{1200-n_2}{1200}$

$n_2=1200×(1-0.0605)≒1127$［min^-1］

答え (4)

2008年（平成20年）問3

巻線形誘導電動機のトルク-回転速度曲線は、電源電圧及び(　ア　)が一定のとき、発生するトルクと回転速度との関係を表したものである。
この曲線は、ある滑りの値でトルクが最大となる特性を示す。このトルクを最大トルク又は(　イ　)トルクと呼んでいる。この最大トルクは(　ウ　)回路の抵抗には無関係である。
巻線形誘導電動機のトルクは(　ウ　)回路の抵抗と滑りの比に関係するので、(　ウ　)回路の抵抗が k 倍になると、前と同じトルクが前の滑りの k 倍の点で起こる。 このような現象は(　エ　)と呼ばれ、巻線形誘導電動機の起動トルクの改善及び速度制御に広く用いられている。

上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる語句として、正しいものを組み合わせたのは次のうちどれか。

	（ア）	（イ）	（ウ）	（エ）
（１）	負荷	臨界	二次	比例推移
（２）	電源周波数	停動	一次	二次励磁
（３）	負荷	臨界	一次	比例推移
（４）	電源周波数	臨界	二次	二次励磁
（５）	電源周波数	停動	二次	比例推移

2008年（平成20年）問3　過去問解説

巻線形誘導電動機のトルク-回転速度曲線は、電源電圧及び(　電源周波数　)が一定のとき、発生するトルクと回転速度との関係を表したものである。
この曲線は、ある滑りの値でトルクが最大となる特性を示す。このトルクを最大トルク又は(　停動　)トルクと呼んでいる。この最大トルクは(　二次　)回路の抵抗には無関係である。
巻線形誘導電動機のトルクは(　二次　)回路の抵抗と滑りの比に関係するので、(　二次　)回路の抵抗が k 倍になると、前と同じトルクが前の滑りの k 倍の点で起こる。 このような現象は(　比例推移　)と呼ばれ、巻線形誘導電動機の起動トルクの改善及び速度制御に広く用いられている。

答え (5)

2008年（平成20年）問15

定格出力 7.5［kW］、定格電圧 220［V］、定格周波数 60［Hz］、8極の三相巻線形誘導電動機がある。この電動機を定格電圧、定格周波数の三相電源に接続して定格出力で運転すると、82［N･m］のトルクが発生する。この運転状態のとき、次の(a)及び(b)に答えよ。

(a) 回転速度［min^-1］の値として、最も近いのは次のうちどれか。

(1) 575　(2) 683　(3) 724　(4) 874　(5) 924

(b) 回転子巻線に流れる電流の周波数［Hz］の値として、最も近いのは次のうちどれか。

(1) 1.74　(2) 4.85　(3) 8.25　(4) 12.4　(5) 155

2008年（平成20年）問15　過去問解説

(a) 電動機のトルクを $T$［N･m］、角速度を $ω$［rad/s］、定格出力を $P$［W］とすれば、回転速度 $n$［min^-1］は、

$P=ωT=2π\displaystyle\frac{n}{60}T$

$7.5×10^3=2π\displaystyle\frac{n}{60}×82$

$n=\displaystyle\frac{60×7.5×10^3}{2π×82}≒874$［min^-1］

答え (4)

(b) 同期速度を $n_s$［min^-1］、すべりを $s$ とすると、

$n_s=\displaystyle\frac{120f_1}{p}=\displaystyle\frac{120×60}{8}=900$［min^-1］

$s=\displaystyle\frac{n_s-n}{n_s}=\displaystyle\frac{900-874}{900}≒0.029$

滑り周波数は、$f_2=sf_1$［Hz］ですので、

$sf_1=0.029×60≒1.74$［Hz］

答え (1)

2009年（平成21年）問15

定格出力 15［kW］、定格電圧 220［V］、定格周波数 60［Hz］、6極の三相誘導電動機がある。この電動機を定格電圧、定格周波数の三相電源に接続して定格出力で運転すると、滑りが 5［%］であった。機械損及び鉄損は無視できるものとして、次の(a)及び(b)に答えよ。

(a) 発生トルク［N･m］の値として、最も近いのは次のうちどれか。

(1) 114　(2) 119　(3) 126　(4) 239　(5) 251

(b) この電動機の発生トルクが上記(a)の 1/2 となったとき、一次銅損は 250［W］であった。このときの効率［%］として、最も近いのは次のうちどれか。
ただし、発生トルクと滑りは比例するものとする。

(1) 92.1　(2) 94.0　(3) 94.5　(4) 95.5　(5) 96.9

2009年（平成21年）問15　過去問解説

(a) 同期速度を $n_s$［min^-1］、回転速度を $n$［min^-1］、すべりを $s$ とすると、

$n_s=\displaystyle\frac{120f}{p}=\displaystyle\frac{120×60}{6}=1200$［min^-1］

$s=\displaystyle\frac{n_s-n}{n_s}$

$0.05=\displaystyle\frac{1200-n}{1200}$

$n=1200×(1-0.05)=1140$

角速度を $ω$［rad/s］、定格出力を $P$［W］とすれば、発生トルクを $T$［N･m］は、

$P=ωT=2π\displaystyle\frac{n}{60}T$

$T=\displaystyle\frac{60×15×10^3}{2π×1140}≒126$［N･m］

答え (3)

(b) 発生トルクが 1/2 となったときのすべりを $s’$ とすると、題意よりすべりはトルクに比例しますので、

$s:s’=1:1/2$
$0.05:s’=1:0.5$
$s’=0.025$

二次入力を $P_2$［W］、出力を$P_o$［W］とすると、

$P_2=2π\displaystyle\frac{n_s}{60}T=2π\displaystyle\frac{1200}{60}×126≒7913$［W］

$P_o=(1-s’)P_2=(1-0.025)×7913≒7715$［W］

効率 $η$［%］は、$\displaystyle\frac{出力}{入力}×100$ で、求めることができます。一次入力を $P_1$［W］、機械出力を$P_o$［W］とし、一次銅損 $P_{c1}$［W］、二次銅損 $P_{c2}$［W］すると、

$P_1=P_{c1}+P_{c2}+P_o=P_{c1}+P_2$

$η=\displaystyle\frac{P_o}{P_1}×100=\displaystyle\frac{P_o}{P_{c1}+P_2}×100$

　$=\displaystyle\frac{7715}{250+7913}×100≒94.5$［%］

答え (3)

2010年（平成22年）問3

次の文章は、三相の誘導機に関する記述である。
固定子の励磁電流による同期速度の(　ア　)と回転子との速度の差(相対速度)によって回転子に電圧が発生し、その電圧によって回転子に電流が流れる。トルクは回転子の電流と磁束とで発生するので、トルク特性を制御するため、巻線形誘導機では回転子巻線の回路をブラシと(　イ　)で外部に引き出して二次抵抗値を調整する方式が用いられる。回転子の回転速度が停止(滑り s=1 )から同期速度(滑り s=0 )の間、すなわち、 1 > s > 0 の運転状態では、磁束を介して回転子の回転方向にトルクが発生するので誘導機は(　ウ　)となる。回転子の速度が同期速度より高速の場合、磁束を介して回転子の回転とは逆の方向にトルクが発生し、誘導機は（　エ　）となる。

上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる語句として、正しいものを組み合わせたのは次のうちどれか。

	(ア)	(イ)	(ウ)	(エ)
（１）	交番磁界	スリップリング	電動機	発電機
（２）	回転磁界	スリップリング	電動機	発電機
（３）	交番磁界	整流子	発電機	電動機
（４）	回転磁界	スリップリング	発電機	電動機
（５）	交番磁界	整流子	電動機	発電機

2010年（平成22年）問3　過去問解説

固定子の励磁電流による同期速度の(　回転磁界　)と回転子との速度の差(相対速度)によって回転子に電圧が発生し、その電圧によって回転子に電流が流れる。トルクは回転子の電流と磁束とで発生するので、トルク特性を制御するため、巻線形誘導機では回転子巻線の回路をブラシと(　スリップリング　)で外部に引き出して二次抵抗値を調整する方式が用いられる。回転子の回転速度が停止(滑り s=1 )から同期速度(滑り s=0 )の間、すなわち、 1 > s > 0 の運転状態では、磁束を介して回転子の回転方向にトルクが発生するので誘導機は(　電動機　)となる。回転子の速度が同期速度より高速の場合、磁束を介して回転子の回転とは逆の方向にトルクが発生し、誘導機は（　発電機　）となる。

答え (2)

2010年（平成22年）問4

極数4で 50［Hz］用巻き線形三相誘導電動機があり、全負荷時の滑りは 4［%］である。全負荷トルクのまま、この電動機の回転速度を 1200［min^-1］にするために、二次回路に挿入する1相当りの抵抗［Ω］の値として、最も近いのは次のうちどれか。
ただし、巻線形三相誘導電動機の二次巻線は星型(Y)結線であり、各相の抵抗値は 0.5Ω とする。

(1) 2.0　(2) 2.5　(3) 3.0　(4) 7.0　(5) 7.5

2010年（平成22年）問4　過去問解説

(a) 同期速度を $n_s$［min^-1］とすると、回転速度を $n’=1200$［min^-1］のときのすべり $s’$ は、

$n_s=\displaystyle\frac{120f}{p}=\displaystyle\frac{120×50}{4}=1500$［min^-1］

$s’=\displaystyle\frac{n_s-n’}{n_s}=\displaystyle\frac{1500-1200}{1500}=0.2$

二次回路に挿入する抵抗を ${r_2}’$［Ω］とすると、すべりは抵抗と比例推移しますので、

$\displaystyle\frac{0.5}{s}=\displaystyle\frac{0.5+{r_2}’}{ s’ }$

$\displaystyle\frac{0.5}{0.04}=\displaystyle\frac{0.5+{r_2}’}{ 0.2 }$

${r_2}’ =2.0$［Ω］

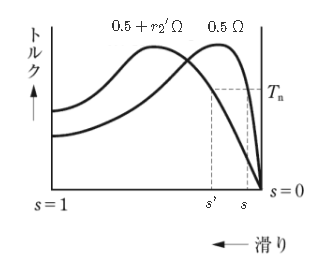
答え (1)

2012年（平成24年）問3

誘導電動機に関する記述として、誤っているものを次の(1)～(5)のうちから一つ選べ。
ただし、誘導電動機の滑りを s とする。

1. 誘導電動機の一次回路には同期速度の回転磁界、二次回路には同期速度の s 倍の回転磁界が加わる。したがって、一次回路と二次回路の巻数比を 1 とした場合、二次誘導起電力の周波数及び電圧は一次誘導起電力の s 倍になる。
2. s が小さくなると、二次誘導起電力の周波数及び電圧が小さくなるので、二次回路に流れる電流が小さくなる。この変化を電気回路に表現するため、誘導電動機の等価回路では、二次回路の抵抗の値を 1/s 倍にして表現する。
3. 誘導電動機の等価回路では、一次巻線の漏れリアクタンス、一次巻線の抵抗、二次巻線の漏れリアクタンス、二次巻線の抵抗、及び電動機出力を示す抵抗が直列回路で表されるので、電動機の力率は 1 にはならない。
4. 誘導電動機の等価回路を構成するリアクタンス値及び抵抗値は、電圧が変化しても s が一定ならば変わらない。s 一定で駆動電圧を半分にすれば、等価回路に流れる電流が半分になり、電動機トルクは半分になる。
5. 同期速度と電動機トルクとで計算される同期ワット（二次入力）は、二次銅損と電動機出力との和となる。

2012年（平成24年）問3　過去問解説

誘導電動機のトルク $T$［N･m］は、滑り $s$ が一定であれば、一次電圧 $V_1$［V］の 2乗に比例します。(4)の記述で、等価回路に流れる電流が半分になると、電圧は 2倍になり、電動機トルクは 1/4 倍になります。したがって、(4)の記述が誤りです。

答え (4)

2012年（平成24年）問5

次の文章は、電動機と負荷のトルク特性の関係について述べたものである。

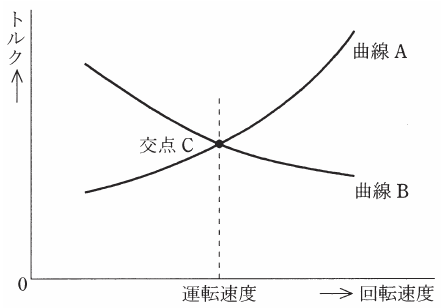
横軸が回転速度、縦軸がトルクを示す図において2本の曲線 A、B は、一方が電動機トルク特性、他方が負荷トルク特性を示している。
いま、曲線 A が（　ア　）特性、曲線 B が（　イ　）特性のときは、2本の曲線の交点 C は不安定な運転点である。これは、何らかの原因で電動機の回転速度がこの点から下降すると、電動機トルクと負荷トルクとの差により電動機が（　ウ　）されるためである。具体的に、電動機が誘導電動機であり、回転速度に対してトルクが変化しない定トルク特性の負荷のトルクの大きさが、誘導電動機の始動トルクと最大トルクとの間にある場合を考える。このとき、電動機トルクと負荷トルクとの交点は、回転速度零と最大トルクの回転速度との間、及び最大トルクの回転速度と同期速度との間の2箇所にある。交点 C は、（　エ　）との間の交点に相当する。

上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

	(ア)	(イ)	(ウ)	(エ)
（１）	電動機トルク	負荷トルク	減速	回転速度零と最大トルクの回転速度
（２）	電動機トルク	負荷トルク	減速	最大トルクの回転速度と同期速度
（３）	負荷トルク	電動機トルク	減速	回転速度零と最大トルクの回転速度
（４）	負荷トルク	電動機トルク	加速	回転速度零と最大トルクの回転速度
（５）	負荷トルク	電動機トルク	加速	最大トルクの回転速度と同期速度

2012年（平成24年）問5　過去問解説

横軸が回転速度、縦軸がトルクを示す図において2本の曲線 A、B は、一方が電動機トルク特性、他方が負荷トルク特性を示している。
いま、曲線 A が（　電動機トルク　）特性、曲線 B が（　負荷トルク　）特性のときは、2本の曲線の交点 C は不安定な運転点である。これは、何らかの原因で電動機の回転速度がこの点から下降すると、電動機トルクと負荷トルクとの差により電動機が（　減速　）されるためである。具体的に、電動機が誘導電動機であり、回転速度に対してトルクが変化しない定トルク特性の負荷のトルクの大きさが、誘導電動機の始動トルクと最大トルクとの間にある場合を考える。このとき、電動機トルクと負荷トルクとの交点は、回転速度零と最大トルクの回転速度との間、及び最大トルクの回転速度と同期速度との間の2箇所にある。交点 C は、（　回転速度零と最大トルクの回転速度　）との間の交点に相当する。

答え (1)

2015年（平成27年）問15

定格出力 15kW、定格電圧 220V、定格周波数 60Hz、6極の三相巻線形誘導電動機がある。二次巻線は星形（Y）結線でスリップリングを通して短絡されており、各相の抵抗値は 0.5Ω である。この電動機を定格電圧、定格周波数の電源に接続して定格出力（このときの負荷トルクをTnとする）で運転しているときの滑りは 5％であった。計算に当たっては、L形簡易等価回路を採用し、機械損及び鉄損は無視できるものとして、次の(a)及び(b)の問に答えよ。

(a) 速度を変えるために、この電動機の二次回路の各相に 0.2Ω の抵抗を直列に挿入し、上記と同様に定格電圧、定格周波数の電源に接続して上記と同じ負荷トルク Tn で運転した。このときの滑りの値［%］として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1) 3.0　(2) 3.6　(3) 5.0　(4) 7.0　(5) 10.0

(b) 電動機の二次回路の各相に上記(a)と同様に 0.2Ω の抵抗を直列に挿入したままで、電源の周波数を変えずに電圧だけを 200V に変更したところ、ある負荷トルクで安定に運転した。このときの滑りは上記(a)と同じであった。この安定に運転したときの負荷トルクの値［N･m］として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1) 99　(2) 104　(3) 106　(4) 109　(5) 114

2015年（平成27年）問15　過去問解説

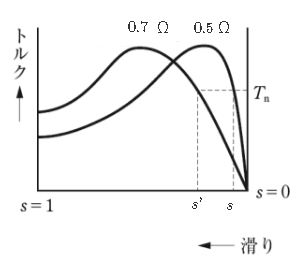
(a) 二次回路に挿入する前後の抵抗と、すべりは比例推移しますので、

$\displaystyle\frac{0.5}{s}=\displaystyle\frac{0.7}{ s’ }$

$\displaystyle\frac{0.5}{0.05}=\displaystyle\frac{0.7}{ s’ }$

$s’=0.07$（7％）

答え (4)

(b) 同期速度を $n_s$［min^-1］とすると、

$n_s=\displaystyle\frac{120f}{p}=\displaystyle\frac{120×60}{6}=1200$［min^-1］

すべり5％で運転しているときの回転速度を $n$［min^-1］、トルクを $T$［N･m］とすると、

$s=\displaystyle\frac{n_s-n}{n_s}$

$0.05=\displaystyle\frac{1200-n}{1200}$

$n=1200×(1-0.05)=1140$［min^-1］

$T=\displaystyle\frac{60}{2π}・\displaystyle\frac{P_o}{n}=\displaystyle\frac{60}{2π}・\displaystyle\frac{15×10^3}{1140}≒125.7$［N･m］

トルクは電圧の 2乗に比例しますので、 負荷トルクを$T’$［N･m］とすると、

$T’=\left(\displaystyle\frac{200}{220}\right)^2×T=\left(\displaystyle\frac{200}{220}\right)^2×125.7≒104$［N･m］

答え (2)

2016年（平成28年）問4

定格周波数 50Hz、6極のかご形三相誘導電動機があり、トルク 200N・m、機械出力 20kW で定格運転している。このときの二次入力（同期ワット）の値［kW］として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1) 19　(2) 20　(3) 21　(4) 25　(5) 27

2016年（平成28年）問4　過去問解説

同期速度を $n_s$［min^-1］とすると、

$n_s=\displaystyle\frac{120f}{p}=\displaystyle\frac{120×50}{6}=1000$［min^-1］

電動機のトルクを $T$［N･m］、角速度を $ω$［rad/s］、二次入力を $P_2$［W］とすれば、

$P_2=ωT=2π\displaystyle\frac{n_s}{60}T=2π\displaystyle\frac{1000}{60}×200=21$［kW］

答え (3)

2017年（平成29年）問15

定格出力 15kW、定格電圧 400V、定格周波数 60Hz、極数4の三相誘導電動機がある。この誘導電動機が定格電圧、定格周波数で運転されているとき、次の(a)及び(b)の問に答えよ。

(a) 軸出力が 15kW、効率と力率がそれぞれ 90% で運転されているときの一次電流の値［A］として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1) 22　(2) 24　(3) 27　(4) 33　(5) 46

(b) この誘導電動機が巻線形であり、全負荷時の回転速度が 1746 min^-1 であるものとする。二次回路の各相に抵抗を追加して挿入したところ、全負荷時の回転速度が 1455 min^-1 となった。ただし、負荷トルクは回転速度によらず一定とする。挿入した抵抗の値は元の二次回路の抵抗の値の何倍であるか。最も近いものを次の(1)～(5)のうちから一つ選べ。

(1) 1.2　(2) 2.2　(3) 5.4　(4) 6.4　(5) 7.4

2017年（平成29年）問15　過去問解説

（(a) 出力を $P$［W］、電圧を $V$［V］、電流を $I$［A］、力率を $cosθ$、効率を $η$ とすると、

$P=\sqrt{3}VIcosθη$［W］

$15×10^3=\sqrt{3}×400×I×0.9×0.9$［W］

$I=\displaystyle\frac{15×10^3}{\sqrt{3}×400×0.9×0.9}≒27$［A］

答え (3)

(b) 同期速度を $n_s$［min^-1］とすると、

$n_s=\displaystyle\frac{120f}{p}=\displaystyle\frac{120×60}{4}=1800$［min^-1］

回転速度を $n=1746$［min^-1］のときのすべり $s$ は、

$s=\displaystyle\frac{n_s-n}{n_s}=\displaystyle\frac{1800-1746}{1800}=0.03$

回転速度を $n’=1455$［min-¹］のときのすべり $s’$ は、

$s’=\displaystyle\frac{n_s-n’}{n_s}=\displaystyle\frac{1800-1455}{1800}≒0.192$

元の二次回路の抵抗を $r$、挿入した抵抗の値を $r’$ とすると、すべりと抵抗は、比例推移しますので、

$\displaystyle\frac{r}{s}=\displaystyle\frac{r+r’}{ s’ }$
$rs’=rs+r’s$
$r’s=r(s’-s)$
$\displaystyle\frac{r’}{r}=\displaystyle\frac{s’-s}{s}=\displaystyle\frac{0.192-0.03}{0.03}=5.4$

答え (3)