このページでは、三相同期電動機の原理と特性について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の機械科目で、実際に出題された三相同期電動機の原理と特性の過去問題の解き方も解説しています。
- 三相同期電動機の原理
- 三相同期電動機の特性
- 電験三種-機械(同期機)過去問
- 1998年(平成10年)問2
- 1998年(平成10年)問2 過去問解説
- 2002年(平成14年)問12
- 2002年(平成14年)問12 過去問解説
- 2005年(平成17年)問5
- 2005年(平成17年)問5 過去問解説
- 2006年(平成18年)問4
- 2006年(平成18年)問4 過去問解説
- 2007年(平成19年)問15
- 2007年(平成19年)問15 過去問解説
- 2011年(平成23年)問5
- 2011年(平成23年)問5 過去問解説
- 2012年(平成24年)問16
- 2012年(平成24年)問16 過去問解説
- 2014年(平成26年)問15
- 2014年(平成26年)問15 過去問解説
- 2016年(平成28年)問5
- 2016年(平成28年)問5 過去問解説
三相同期電動機の原理
三相同期電動機のトルク
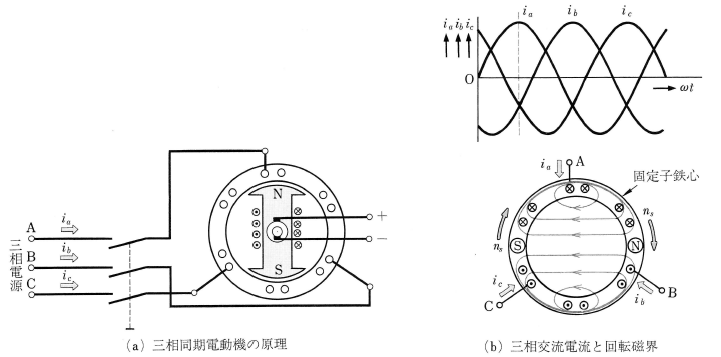
三相同期電動機の構造は、三相同期発電機と同じです。図1(a)は、三相同期電動機の原理図です。固定子の三相巻線に三相交流電流 $i_a,i_b,i_c$[A]が流れると、図(b)に示すように、回転磁界が発生します。図(b)で、固定子鉄心から磁束の出る部分N極を(N)で表し、磁束が固定子鉄心に入る部分S極を(S)で表すと、(N),(S)は、同期速度で相回転の向きに回転します。
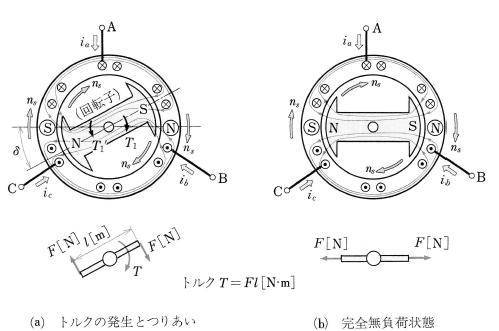
同期電動機が負荷を担って回転しているときは、図2(a)のように、回転子磁極N,Sと回転磁界(N),(S)が $δ$[rad]の角度をへだてた位置関係を保って同期速度で回転しています。このときSと(N)、およびNと(S)との吸引力によって、回転子に時計まわりのトルク $T_1$[N・m]が生じ、$T_1$ に対して逆方向に働く負荷のトルク ${T_1′}$[N・m]に打ち勝って回転します。
次に電動機の負荷が軽くなって、${T_1}’$[N・m]が小さくなると、$δ$[rad]も小さくなり、電動機が無負荷になれば、図(b)のように $δ$ は 0[rad]になって、 ${T_1}’$,$T_1$ も 0[N・m]になり、トルクは発生しません。
このように、回転子磁極は、電機子電流による回転磁界と等しい同期速度で回転し、負荷の増減によって、回転子磁極軸と回転磁界軸との位置関係 $δ$ が変わるようになります。$δ$ は負荷角といいます。
同期速度を求める式
$n_s=\displaystyle\frac{120f}{p}$
$n_s$[min-1]:同期速度
$f$[Hz]:周波数
$p$:固定子の極数
三相同期電動機の出力を求める式①
$P=ωT=2π\displaystyle\frac{n_s}{60}T$
$P$[W]:出力
$ω$[rad/s]:角速度
$T$[N・m]:トルク
$n_s$[min-1]:回転速度
三相同期電動機の等価回路
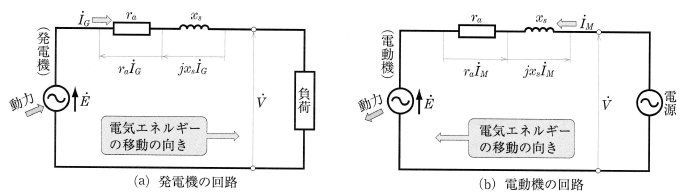
図3(a)は、三相同期発電機の1相分を示す等価回路です。この図において、各電圧の間には次の関係がなりたちます。
$\dot{V}=\dot{E}-r_a\dot{I_G}-jx_s\dot{I_G}=\dot{E}-(r_a+jx_s)\dot{I_G}$
$\dot{E}=\dot{V}+(r_a+jx_s)\dot{I_G}$ … (1)
三相同期電動機は、構造的に同期発電機と同じですので、その1相分についての等価回路は図(b)となります。$\dot{V}$[V]は1相分の供給電圧であり、$\dot{E}$[V]は、回転する磁極によって誘導される電機子巻線1相分の起電力です。電動機電流 $\dot{I_M}$[A]の向きを図のように定めると、この回路では、同期電動機として、各電圧の間には、次の関係がなりたちます。
$\dot{V}=\dot{E}+r_a\dot{I_M}+jx_s\dot{I_M}=\dot{E}+(r_a+jx_s)\dot{I_M}$
$\dot{E}=\dot{V}-(r_a+jx_s)\dot{I_M}$ … (2)
したがって、式(1)より、三相同期発電機の起電力は供給電圧とインピーダンス降下のベクトル和になり、式(2)より、三相同期電動機の起電力は供給電圧とインピーダンス降下のベクトル差になります。
電機子反作用
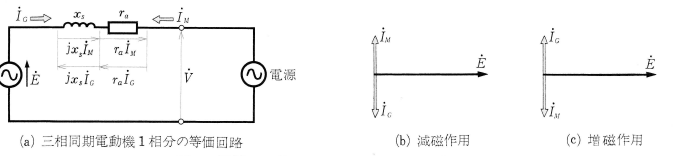
図4(a)は、三相同期電動機1相分の等価回路です。電流 $\dot{I_G}$[A]の向きを図のように考えると、$\dot{I_M}=-\dot{I_G}$ であり、$\dot{E}$[V]に対して、$\displaystyle\frac{π}{2}$[rad]の位相差をもつ場合のベクトル図は、図(b),(c)となります。
$\dot{E}$[V]と $\dot{I_G}$[A]は、図3(a)の同期発電機の回路と同じです。$\dot{E}$[V]と $\dot{I_G}$[A]の関係が、図4(b)のときは、電機子反作用は「減磁作用」として働き、図(c)のときは、「増磁作用」として働きます。
ここで、電機子電流を $\dot{I_M}$[A]で表せば、同期電動機における電機子反作用は、$\dot{E}$[V]に対し、$\displaystyle\frac{π}{2}$[rad]だけ進んだ電流によって減磁作用(図(b))として働き、$\displaystyle\frac{π}{2}$[rad]だけ遅れた電流によって増磁作用(図(c))として働きます。また、$\dot{E}$[V]に対し、同相の電流 $\dot{I_M}$[A]は、「交さ磁化作用」として働きます。
これらの作用は、回路的にはリアクタンスであり、同期発電機の場合と同じように、漏れリアクタンスとあわせて同期リアクタンスといいます。図3(b)と図4(a)の $x_s$[Ω]は同期リアクタンスです。
| 起電力 E と電機子電流 I の関係 | 同期発電機 | 同期電動機 |
|---|---|---|
| 同相 | 交さ磁化作用 | 交さ磁化作用 |
| 遅れ | 減磁作用 | 増磁作用 |
| 進み | 増磁作用 | 減磁作用 |
三相同期電動機の特性
入力・出力・トルク
ふつう同期電動機では、電機子巻線の抵抗 $r_a$[Ω]は同期リアクタンス $x_s$[Ω]に比べて非常に小さいので、$r_a$[Ω]を無視して考えると、三相同期電動機の1相分の等価回路は図6(a)となり、そのベクトル図は図(b)となります。ここで、$δ$[rad]は、$\dot{V}$[V]に対する $\dot{E}$[V]の位相差で負荷角であり、$θ$[rad]は、$\dot{V}$[V]に対する $\dot{I_M}$[A]の位相差です。
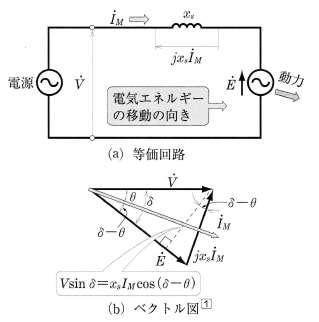
入力
図6(b)のベクトル図からわかるように、電動機の力率は $cosθ$ですので、三相同期電動機の1相分の入力 $P_1$[W]は、次の式で表すことができます。
$P_1=VI_Mcosθ$[W]
出力
図6の $\dot{E}$ と $\dot{I_M}$ の関係は、ベクトル図では正の電力ですが、回路図ではその向きがたがいに逆ですので、発生電力ではなく、消費電力、すなわち出力を表します。そこで、三相同期電動機1相分の出力 $P_o$[W]は、次の式で表わすことができます。
$P_o=EI_Mcos(δ-θ)=\displaystyle\frac{VE}{x_s}sinδ$[W]
同期電動機の一相分の出力を求める式
$P_o=EI_Mcos(δ-θ)=\displaystyle\frac{VE}{x_s}sinδ$
$P_o$[W]:一相分の出力
$E$[V]:電機子巻線に発生する一相分の誘導起電力
$I_M$[A]:一相に流れる電流
$δ$:負荷角
$θ$:力率角
$V$:一相分の端子電圧
$x_s$[Ω]:同期リアクタンス
三相同期電動機の出力を求める式②
$P=\displaystyle\frac{3VE}{x_s}sinδ=2π\displaystyle\frac{n_s}{60}T=ωT$
$P$[W]:三相同期電動機の出力
$E$[V]:電機子巻線に発生する誘導起電力
$V$:端子電圧
$x_s$[Ω]:同期リアクタンス
$n_s$[min-1]:回転速度
$ω$[rad/s]:角速度
$T$[N・m]:トルク
トルク
同期電動機の一相分の出力を求める式から、三相同期電動機の全出力 $P$[W]は $3P_o$[W]となります。このときの電動機の同期速度を $n_s$[min-1]とすると、トルク $T$[N・m]は、次の式で表すことができます。
$P=3P_o=2π\displaystyle\frac{n_s}{60}T$
$T=\displaystyle\frac{60}{2πn_s}・3P_o=\displaystyle\frac{60}{2πn_s}・\displaystyle\frac{3VE}{x_s}sinδ$ … (5)
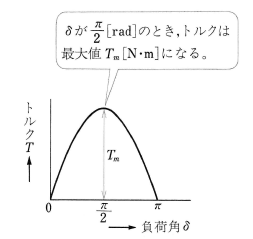
以上のことから、図7に示すように、負荷角 $δ$ が大きくなるに従ってトルク $T$[N・m]は大きくなり、$δ$が $\displaystyle\frac{π}{2}$[rad]のとき最大値 $T_m$[N・m]となります。負荷のトルクが $T_m$[N・m]より大きいと、さらに $δ$ は増加し、トルクは減少して、電動機はついに停止します。これを「同期外れ」といい、同期外れをしない最大トルク $T_m$[N・m]を「脱出トルク」といいます。脱出トルクは、実際には $δ$ が 50~ 60° の範囲にあって、電動機が定格周波数・定格電圧および常規の励磁において、運転を1分間継続できる最大トルクのことです。
同期電動機において、負荷が急変すると、負荷角 $δ$ が変化し、新しい負荷角 $δ′$ に落ちつこうとしても、回転子の慣性のために、負荷角は $δ’$ を中心として周期的に変動します。この現象を「乱調」といい、電源の起電力や周波数などが周期的に変動した場合にも生じます。乱調が激しくなると、電源との同期が外れて電動機は停止します。乱調を防ぐには、始動巻線も兼ねる制動巻線を設けたり、はずみ車を取り付けたりします。
位相特性
三相同期電動機が、供給電圧 $\dot{V}$[V]、電機子電流 $\dot{I_M}$[A]、力率1で運転している場合、ベクトル図は図8(a)となります。ここで、$x_s$[Ω]を界磁電流 $I_f$[A]に無関係に一定と考えると、$\dot{V}$[V]と電動機の1相分の出力 $P_o$[W]が一定であれば、同期電動機の一相分の出力を求める式からわかるように、$Esinδ$ も一定となります。したがって、界磁電流 $I_f$[A]の変化によって増減する誘導起電力 $\dot{E}$[V]のベクトルの先端は、XX’上を移動することになります。そこで、界磁電流を図(a)の状態から変化させた場合の $\dot{I_M}$[A]の位相について考えます。
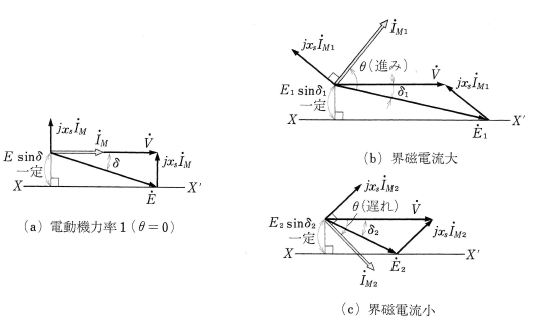
界磁電流 $I_f$ の増加
$I_f$[A]を大きくすると、図(b)からわかるように、$\dot{E}$[V]が大きくなり、$\dot{E_1}$[V]となれば、 $δ$[rad]が $δ_1$[rad]まで減少し、$\dot{I_M}$[A]の大きさが増して $\dot{V}$[V]より位相が進んだ電流 $\dot{I}_{M1}$[A]になります。
界磁電流 $I_f$ の減少
$I_f$[A]を小さくすると、図(C)からわかるように、$\dot{E}$[V]が小さくなり、$\dot{E_2}$[V]となれば、 $δ$[rad]が $δ_2$[rad]まで増加し、$\dot{I_M}$[A]の大きさが増して $\dot{V}$[V]より位相が遅れた電流 $\dot{I}_{M2}$[A]になります。
これらのことから、界磁電流 $I_f$ の大きさによって力率が変化することがわかります。
V曲線( 位相特性曲線 )
図8に示すように、三相同期電動機は界磁電流を変えると、電機子電流の供給電圧に対する位相が変わり、さらに電機子電流の大きさも変わります。そこで、電機子電流 $I_M$[A]を縦軸に、界磁電流 $I_f$[A]を横軸にとってグラフをかくと、図9に示すようにV形の曲線となります。これを同期電動機の位相特性曲線またはV曲線といいます。曲線 A は無負荷の場合、曲線 B,C,D はしだいに負荷を大きくした場合です。これらの曲線の最低点は力率が1に当たる点で、図の破線で示す部分の右側は進み電流、左側は遅れ電流の範囲となります。
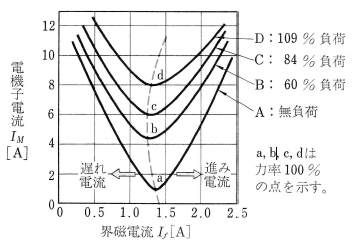
- V曲線中の点線は、各負荷における力率100%の動作点を結んだ線であり、どの負荷においても力率100%のとき、電機子電流が一番小さくなる
- 界磁電流 $I_f$[A]を「力率100%の点線」の位置に相当する値にすれば、力率を100%にすることができる
- V曲線中の「力率100%の点線」より界磁電流 $I_f$[A]を減らすと遅れ、界磁電流を増やすと進みになる(「力率100%の点線」より左側の領域は遅れ、右側の領域は進み)
電験三種-機械(同期機)過去問
1998年(平成10年)問2
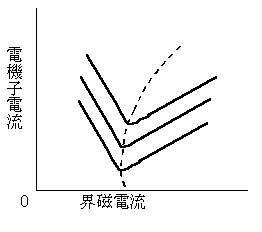
図は、同期電動機の電機子電流を縦軸に、界磁電流を横軸にとって、電機子電流と界磁電流を示したもので、これらの曲線は( ア )と呼ばれている。
これらの曲線には最低線が存在し、その点は( イ )に相当する。負荷が増大すると、この曲線は上方に移動し、最低点はある曲線を描いて変化する。最低点が描く曲線(破線)の右側の部分は( ウ )、左側の部分は( エ )の範囲である。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に記入する字句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 速度特性曲線 | 最小速度 | 加速 | 減速 |
| (2) | 電流特性曲線 | 最小電流 | 遅れ電流 | 進み電流 |
| (3) | 飽和特性電流 | 磁気飽和 | 負飽和 | 飽和 |
| (4) | 位相特性曲線 | 平衡点 | 増磁作用 | 減磁作用 |
| (5) | 位相特性曲線 | 力率1 | 進み力率 | 遅れ力率 |
1998年(平成10年)問2 過去問解説
図は、同期電動機の電機子電流を縦軸に、界磁電流を横軸にとって、電機子電流と界磁電流を示したもので、これらの曲線は( 位相特性曲線 )と呼ばれている。
これらの曲線には最低線が存在し、その点は( 力率1 )に相当する。負荷が増大すると、この曲線は上方に移動し、最低点はある曲線を描いて変化する。最低点が描く曲線(破線)の右側の部分は( 進み力率 )、左側の部分は( 遅れ力率 )の範囲である。
答え (5)
2002年(平成14年)問12
定格電圧 200[V]、定格周波数 60[Hz]、6極の三相同期電動機があり、力率 0.9(進み)、定格 80[%]で運転し、トルク 72[N・m]を発生している。この電動機について、次の(a)及び(b)に答えよ。
(a) このときの出力[kW]の値として、最も近いものは次のうちどれか。
(1) 0.92 (2) 1.4 (3) 5.2 (4) 7.5 (5) 9.0
(b) このときの線電流[A]の値として、最も近いものは次のうちどれか。
(1) 3.7 (2) 19 (3) 30 (4) 36 (5) 63
2002年(平成14年)問12 過去問解説
(a) 同期速度 $N_s=\displaystyle\frac{120×f(周波数)}{p(極数)}$ より、
$N_s=\displaystyle\frac{120×f}{p}=\displaystyle\frac{120×60}{6}=1200$[min-1]
トルクを $T$[N・m]とすると、電動機の出力を $P$[W]は、
$P=2π\displaystyle\frac{N_s}{60}T=2π\displaystyle\frac{1200}{60}×72≒9.0$[kW]
答え (5)
(b) 力率を $cosθ$、効率を $η$[%]とすると、線電流 $I$[A]は、
$P=\sqrt{3}VIcosθ・\displaystyle\frac{η}{100}$
$9×10^3=\sqrt{3}×200I×0.9×\displaystyle\frac{80}{100}$
$I=\displaystyle\frac{9×10^4}{\sqrt{3}×200×0.9×8}≒36$[A]
答え (4)
2005年(平成17年)問5
定格出力 2000[kW]、定格電圧 3.3[kV]、定格周波数 60[Hz]、力率 80[%]、回転速度 240[min-1]と銘板に記載された同期電動機がある。この電動機の極対数として、正しいのは次のうちどれか。
(1) 15 (2) 20 (3) 30 (4) 60 (5) 120
2005年(平成17年)問5 過去問解説
同期速度 $N_s=\displaystyle\frac{120×f(周波数)}{p(極数)}$ より、
$240=\displaystyle\frac{120×60}{p}$
$p=\displaystyle\frac{120×60}{240}=30$
極数が30なので、極対数は 30÷2=15 対
答え (1)
2006年(平成18年)問4
同期電動機が一定の負荷で、力率 1 の状態で運転されている。この状態から、負荷を一定に保って、界磁電流のみを増加させるとき、電機子電流の大きさと同期電動機の力率の変化に関する記述として、正しいのは次のうちどれか。
- 電機子電流は増加し、進み力率になる。
- 電機子電流は増加し、遅れ力率になる。
- 電機子電流は減少し、力率は変化しない。
- 電機子電流は減少し、進み力率になる。
- 電機子電流は変化せず、遅れ力率になる。
2006年(平成18年)問4 過去問解説
同期電動機の界磁電流を増加すると、電機子電流は増加して進み力率となります。
答え (1)
2007年(平成19年)問15
6極、定格周波数 60[Hz]、電機子巻線がY結線の円筒形三相同期電動機がある。この電動機の一相あたりの同期リアクタンスは 3.52[Ω]であり、また電機子抵抗は無視できるものとする。 端子電圧(線間) 440[V]、定格周波数の電源に接続し、励磁電流を一定に保ってこの電動機を運転したとき、次の(a)及び(b)に答えよ。
(a) この電動機の同期速度を角速度[rad/s]で表した値として、最も近いのは次のうちどれか。
(1) 12.6 (2) 48 (3) 63 (4) 126 (5) 253
(b) 無負荷誘導起電力(線間)が 400[V]、負荷角が 60[°]のとき、この電動機のトルク[N・m]の値として、最も近いのは次のうちどれか。
(1) 115 (2) 199 (3) 345 (4) 597 (5) 1034
2007年(平成19年)問15 過去問解説
(a) 同期速度 $N_s=\displaystyle\frac{120×f(周波数)}{p(極数)}$ より、
$N_s=\displaystyle\frac{120×60}{6}=1200$[min-1]
角速度 $ω=\displaystyle\frac{2πN_s}{60}$[rad/s]より、
$ω=\displaystyle\frac{2π×1200}{60}≒126$[rad/s]
答え (4)
(b) 同期リアクタンスを $X_s$[Ω]、端子電圧を $V$[V]、誘導起電力を $E$[V]、角負荷を $δ$ 、1相分の出力を $P_o$[W]とすると、全出力 $P$[W]は、
$P=3P_o=2π\displaystyle\frac{N_s}{60}T$
$P=3P_o=3\displaystyle\frac{VE}{x_s}sinδ$
$= 3×\displaystyle\frac{\displaystyle\frac{440}{\sqrt{3}}× \displaystyle\frac{400}{\sqrt{3}} }{3.52}sin60°$
=$\displaystyle\frac{440×400}{3.52}×\displaystyle\frac{\sqrt{3}}{2}≒43301$[W]
トルクを $T$[N・m]とすると、
$P=ωT$
$43301=126T$
$T≒345$[N・m]
答え (3)
2011年(平成23年)問5
交流電動機に関する記述として,誤っているものを次の(1)~(5)のうちから一つ選べ。
- 同期機と誘導機は、どちらも三相電源に接続された固定子巻線(同期機の場合は電機子巻線、 誘導機の場合は一次側巻線)が、同期速度の回転磁界を発生している。 発生するトルクが回転磁界と回転子との相対位置の関数であれば同期電動機であり、回転磁界と回転子との相対速度の関数であれば誘導電動機である。
- 同期電動機の電機子端子電圧を $V$[V](相電圧実効値)、この電圧から電機子電流の影響を除いた電圧(内部誘導起電力)を $E_o$[V](相電圧実効値)、$V$ と $E_o$ との位相角を $δ$[rad]、同期リアクタンスを $X$[Ω]とすれば、三相同期電動機の出力は、$3×(E_o・\displaystyle\frac{V}{X})sinδ$[W]となる。
- 同期電動機では、界磁電流を増減することによって、入力電力の力率を変えることができる。電圧一定の電源に接続した出力一定の同期電動機の界磁電流を減少していくと、V曲線に沿って電機子電流が増大し、力率 100[%]で電機子電流が最大になる。
- 同期調相機は無負荷運転の同期電動機であり、界磁電流が作る磁束に対する電機子反作用による増磁作用や減磁作用を積極的に活用するものである。
- 同期電動機では、回転子の磁極面に設けた制動巻線を利用して停止状態からの始動ができる。
2011年(平成23年)問5 過去問解説
- 正しい記述です。同期機も誘導機も同期速度の回転磁界を発生しています。同期電動機は、発生トルクが回転磁界と回転子の相対位置の関数です。誘導電動機は、発生トルクが回転磁界と回転子の相対速度の関数です。
- 正しい記述です。三相同期電動機の出力[W]は P=3×V-Eo/Xs で示されます。
- (V:電機子の相電圧 Eo:内部誘導起電力の相電圧 Xs:同期リアクタンス σ:負荷角
- 正しい記述です。同期調相機は無負荷運転の同期電動機であり、電機子反作用の増磁作用や減磁作用を活用したものです。
- 正しい記述です。同期電動機では、回転子の磁極面に設けた制動巻線を利用して始動できます。
(3) 同期電動機の位相特性曲線(V曲線)は、界磁電流を増減して、電機子電流の変化を示したものです。電圧一定の電源に接続した出力一定の同期電動機の界磁電流を減少していくと、V曲線に沿って電機子電流が増減していきます。力率100%で、電機子電流は最小になります。したがって、(3)の記述は誤りです。
答え (3)
2012年(平成24年)問16
三相同期電動機が定格電圧 3.3[kV]で運転している。ただし、三相同期電動機は星形結線で1相当たりの同期リアクタンスは 10[Ω]であり、電機子抵抗、損失及び磁気飽和は無視できるものとする。次の(a)及び(b)の問に答えよ。
(a) 負荷電流(電機子電流) 110[A]、力率cosφ=1で運転しているときの1相当たりの内部誘導起電力[V]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 1100 (2) 1600 (3) 1900 (4) 2200 (5) 3300
(b) 上記(a)の場合と電圧及び出力は同一で、界磁電流を1.5倍に増加したときの負荷角(電動機端子電圧と内部誘導起電力との位相差)をδ’とするとき、sinδ’の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.250 (2) 0.333 (3) 0.500 (4) 0.707 (5) 0.866
2012年(平成24年)問16 過去問解説
(a) 三相同期電動機の1相分の等価回路とベクトル図を示します。
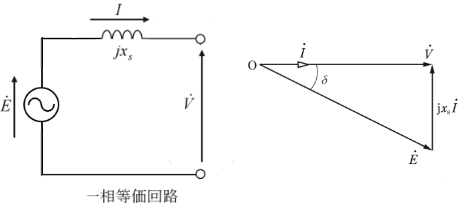
ベクトル図より、
$E=\sqrt{V^2+(x_sI)^2}$
$=\sqrt{(\displaystyle\frac{3300}{\sqrt{3}})^2+(10×110)^2}=2200$[V]
答え (4)
(b) 界磁電流増加前の sinδ は、(a)のベクトル図より
$sinδ=\displaystyle\frac{x_sI}{E}=\displaystyle\frac{10×110}{2200}=0.5$
三相同期電動機1相分の出力 $P$[W]は、
$P=EI_Mcos(δ-θ)=\displaystyle\frac{VE}{x_s}sinδ=\displaystyle\frac{0.5VE}{x_s}$
界磁電流増加後の1相分の出力 $P’$[W]は、
$P’=\displaystyle\frac{1.5VE}{x_s}sinδ’$
題意より、$P=P’$ ですので、
$\displaystyle\frac{0.5VE}{x_s}=\displaystyle\frac{1.5VE}{x_s}sinδ’$
$sinδ’=\displaystyle\frac{0.5}{1.5}≒0.333$
答え (2)
2014年(平成26年)問15
周波数が 60Hz の電源で駆動されている4極の三相同期電動機(星形結線)があり、端子の相電圧 $V$[V]は $\displaystyle\frac{400}{\sqrt{3}}V$、電機子電流 $I_M$[A]は 200A、力率 1で運転している。1相の同期リアクタンス $X_s$[Ω]は 1.00Ω であり、電機子の巻線抵抗、及び機械損などの損失は無視できるものとして、次の(a)及び(b)の問に答えよ。
(a) 上記の同期電動機のトルクの値[N・m]として最も近いものを、次の(1)~(5)のうちから一つ選べ。
(1) 12.3 (2) 368 (3) 735 (4) 1270 (5) 1470
(b) 上記の同期電動機の端子電圧及び出力を一定にしたまま界磁電流を増やしたところ、電機子電流が $I_{M1}$[A]に変化し、力率 $cosθ$ が $\displaystyle\frac{\sqrt{3}}{2}$(θ=30°)の進み負荷となった。出力が一定なので入力電力は変わらない。図はこのときの状態を説明するための1相の概略のベクトル図である。このときの1相の誘導起電力 $E$[V]として、最も近い $E$ の値を次の(1)~(5)のうちから一つ選べ。
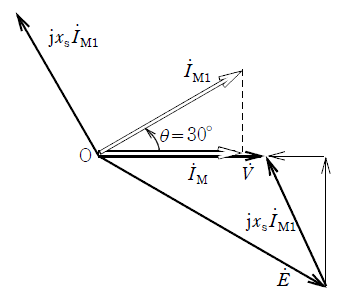
(1) 374 (2) 387 (3) 400 (4) 446 (5) 475
2014年(平成26年)問15 過去問解説
(a) 同期速度 $N_s=\displaystyle\frac{120×f(周波数)}{p(極数)}$ より、
$N_s=\displaystyle\frac{120×60}{4}=1800$[min-1]
角速度 $ω=\displaystyle\frac{2πN_s}{60}$[rad/s]より、
$ω=\displaystyle\frac{2π×1800}{60}=60π$[rad/s]
三相出力を $P$[W]とすると、
$P=3VI_Mcosθ=3×\displaystyle\frac{400}{\sqrt{3}}×200×1≒138.6$[kW]
トルクを $T$[N・m]とすると、
$P=ωT$
$138.6×10^3=60πT$
$T≒735$[N・m]
答え (3)
(b) ベクトル図を示します。
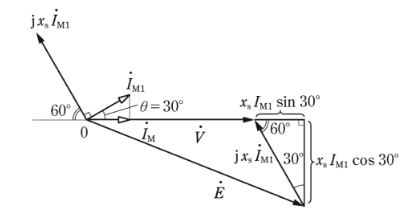
図より、 $I_M=I_{M1}cosθ$ ですので、
$200=I_{M1}×\displaystyle\frac{\sqrt{3}}{2}$
$I_{M1}=\displaystyle\frac{400}{\sqrt{3}}$
1相の誘導起電力 $E$[V]は、
$E=\sqrt{(V+x_sI_{M1}sin30°)^2+(x_sI_{M1}cos30°)^2}$
$=\sqrt{(\displaystyle\frac{400}{\sqrt{3}}+1.0×\displaystyle\frac{400}{\sqrt{3}}×\displaystyle\frac{1}{2})^2+(1.0×\displaystyle\frac{400}{\sqrt{3}}×\displaystyle\frac{\sqrt{3}}{2})^2}$
$=\sqrt{(\displaystyle\frac{400}{\sqrt{3}}+\displaystyle\frac{200}{\sqrt{3}})^2+(200)^2}=400$[V]
答え (3)
2016年(平成28年)問5
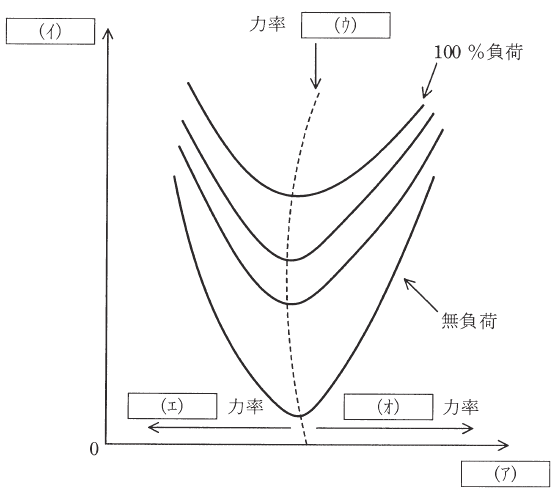
次の文章は、同期電動機の特性に関する記述である。記述中の空白箇所の記号は、図中の記号と対応している。
図は同期電動機の位相特性曲線を示している。形がVの字のようになっているのでV曲線とも呼ばれている。横軸は( ア )、縦軸は( イ )で、負荷が増加するにつれ曲線は上側へ移動する。図中の破線は、各負荷における力率( ウ )の動作点を結んだ線であり、この破線の左側の領域は( エ )力率、右側の領域は( オ )力率の領域である。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (1) | (2) | (3) | (4) | (5) | |
| (1) | 電機子電流 | 界磁電流 | 1 | 遅 れ | 進 み |
| (2) | 界磁電流 | 電機子電流 | 1 | 遅 れ | 進 み |
| (3) | 界磁電流 | 電機子電流 | 1 | 進 み | 遅 れ |
| (4) | 電機子電流 | 界磁電流 | 0 | 進 み | 遅 れ |
| (5) | 界磁電流 | 電機子電流 | 0 | 遅 れ | 進 み |
2016年(平成28年)問5 過去問解説
図は同期電動機の位相特性曲線を示している。形がVの字のようになっているのでV曲線とも呼ばれている。横軸は( 界磁電流 )、縦軸は( 電機子電流 )で、負荷が増加するにつれ曲線は上側へ移動する。図中の破線は、各負荷における力率( 1 )の動作点を結んだ線であり、この破線の左側の領域は( 遅れ )力率、右側の領域は( 進み )力率の領域である。
答え (2)





