第二種電気工事士の筆記試験に初心者の方でも簡単に独学で合格する勉強方法を紹介しています。第二種電気工事士の筆記試験は、過去問から繰り返し出題されていますので、出題分野毎に過去問をまとめて解くことで、効果的な勉強方法となります。このページでは、配電理論及び配線設計「電圧降下と電力損失」について、解説しています。
- 電圧降下と電力損失
- 配電理論及び配線設計:第二種電気工事士 過去問
- 問1 単相2線式回路の電圧降下と電力損失①
- 問2 単相2線式回路の電圧降下と電力損失②
- 問3 単相2線式回路の電圧降下と電力損失③
- 問4 単相2線式回路の電圧降下と電力損失④
- 問5 単相2線式回路の電圧降下と電力損失⑤
- 問6 単相3線式回路の電圧降下と電力損失①
- 問7 単相3線式回路の電圧降下と電力損失②
- 問8 単相3線式回路の電圧降下と電力損失③
- 問9 単相3線式回路の電圧降下と電力損失④
- 問10 単相3線式回路の電圧降下と電力損失⑤
- 問11 三相交流回路の電圧降下と電力損失①
- 問12 三相交流回路の電圧降下と電力損失②
- 問13 三相交流回路の電圧降下と電力損失③
- 問14 三相交流回路の電圧降下と電力損失④
- 問15 三相交流回路の電圧降下と電力損失⑤
- 問16 電線の太さ
電圧降下と電力損失
配電路で電気を送る場合、電線の抵抗分は無視することができません。この抵抗分は、電圧降下を引き起こします。また、電線の抵抗分で電力が消費されてしまうことがあります。これを電力損失(抵抗損)といいます。
線路の抵抗を $r$、流れる電流を $I$とすると、1線当たりの電圧降下と電力損失は次の式で表わすことができます。
1線当たりの電圧降下と電力損失
電圧降下:$v=IR$
電力損失:$P_L=I^2r$
(PL:Lossの ”L” )
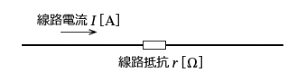
この損失は熱エネルギーとなり、電線温度を上昇させる原因になります。
単相2線式の電圧降下と電力損失
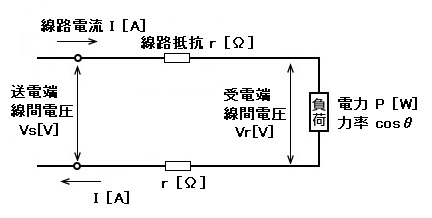
Vs:送電端の線間電圧[V](supplyの”s”)
Vr:受電端の線間電圧[V](receiveの”r”)
電圧降下
$v=Vs-Vr=2Ir$
電力損失
$P_L = 2I^2r = \displaystyle \frac{ 2P^2r }{ (Vrcosθ)^2 } $
電線2本分で考えます。
単相3線式の電圧降下と電力損失
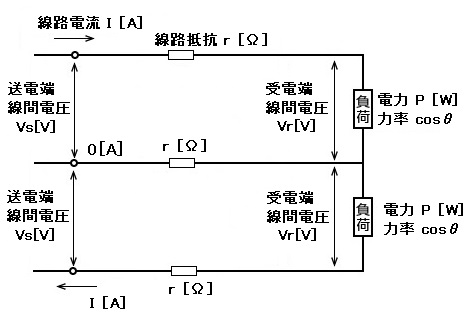
電圧降下
$v=Vs-Vr=2Ir$
電力損失
$P_L = 2I^2r = \displaystyle \frac{ 2P^2r }{ (Vrcosθ)^2 } $
平衡負荷の場合、中性線に電流が流れませんので電線2本分で考えます。
三相3線式の電圧降下と電力損失
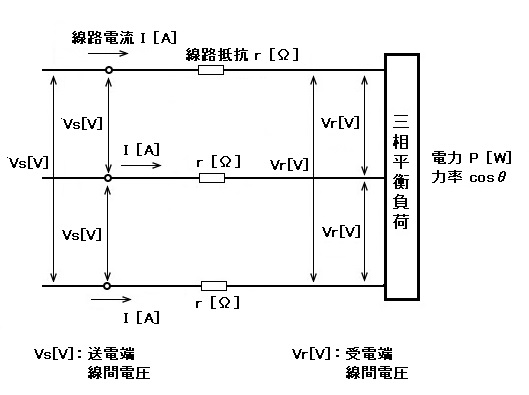
電圧降下
$v=Vs-Vr=\sqrt{3}Ir$
電力損失
$P_L = 3I^2r = \displaystyle \frac{ P^2r }{ (Vrcosθ)^2 } $
電線3本分で考えます。
配電理論及び配線設計:第二種電気工事士 過去問
(財)電気技術者試験センターが作成した第二種電気工事士の筆記試験に出題された問題です。
問1 単相2線式回路の電圧降下と電力損失①
図のように、電線のこう長 L[m]の配線により,抵抗負荷に電力を供給した結果、負荷電流が 10A であった。配線における電圧降下 V1 – V2[V]を表す式として、正しいものは。
ただし、電線の電気抵抗は長さ 1m 当たり r[Ω]とする。
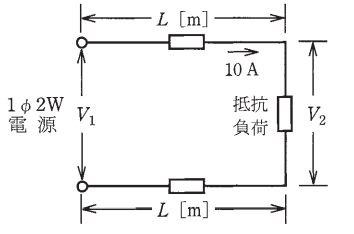
イ. rL ロ. 2rL ハ. 10rL 二. 20rL
こう長 L[m]の電線の抵抗は rL[Ω]ですので、電圧降下 $V_1 – V_2$[V]は、
$V_1 – V_2=2×rL×10=20rL$[V]
答え(二)
2012年(平成24年)下期 問7 類似
2017年(平成29年)下期 問6
問2 単相2線式回路の電圧降下と電力損失②
図のように、電線のこう長 16[m]の配線により、消費電力 2000[W]の抵抗負荷に電力を供給した結果、負荷の両端の電圧は 100[V]であった。配線における電圧降下[V]は。
ただし、電線の電気抵抗は長さ 1000[m]当たり 3.2[Ω]とする。
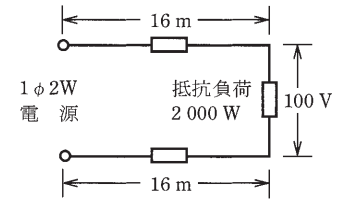
イ. 1 ロ. 2 ハ. 3 二. 4
消費電力を $P$ [W]、負荷の両端の電圧を $V$[V]とすると、回路に流れる電流 $I$[A]は、
$I=\displaystyle\frac{P}{V}=\displaystyle\frac{2000}{100}=20$[A]
電線 1本分の抵抗 $r$[Ω]は、
$r=16×\displaystyle\frac{3.2}{1000}=0.0512$[Ω]
電圧降下 $v$[V]は、
$v=2Ir=2×20×0.0512≒2$[V]
答え(ロ)
2007年(平成19年)問6
2010年(平成22年)問7 類似
2017年(平成29年)上期 問6 類似
2018年(平成30年)上期 問6
2018年(平成30年)下期 問6
問3 単相2線式回路の電圧降下と電力損失③
図のような単相交流回路で、抵抗負荷の消費電力[kW]は。
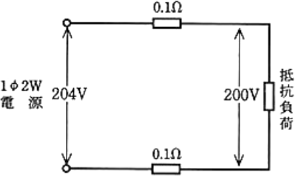
イ. 1 ロ. 2 ハ. 3 二. 4
電圧降下を $v$[V]とすると、
$v=Vs-Vr=204-200=4$[V]
回路に流れる電流 $I$[A]は、$v=2Ir$ より、
$I=\displaystyle\frac{v}{2r}=\displaystyle\frac{4}{2×0.1}=20$[A]
抵抗負荷の消費電力 $P$[kW]は、
$P=VrI=200×20=4$[kW]
答え(二)
2007年(平成19年)問4
問4 単相2線式回路の電圧降下と電力損失④
図のような単相2線式回路で、c-c’ 間の電圧が99 Vのとき、a-a’ 間の電圧[V]は。
ただし、 r は電線の抵抗[Ω]とする。
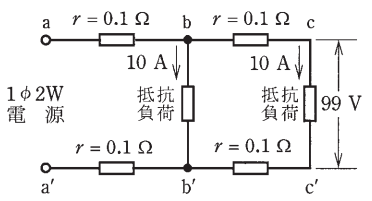
イ. 102 ロ. 103 ハ. 104 二. 105
b-b’ 間の電圧を $V_b$[V]、電圧降下を $v_b$[V]とすると、
$v_b=V_b-V_c=V_b-99$[V]
$v_b=2Ir=2×10×0.1=2$[V]
∴$V_b=101$[V]
a-a’ 間の電圧を $V_a$[V]、電圧降下を $v_a$[V]とすると、
$v_a=V_a-V_b=V_a-101$[V]
$v_a=2Ir=2×(10+10)×0.1=4$[V]
∴$V_a=105$[V]
答え(二)
2015年(平成27年)下期 問6
問5 単相2線式回路の電圧降下と電力損失⑤
図のように単相2線式回路において、c-c’ 間の電圧が100[V]のとき、a-a’ 間の電圧[V]は。
ただし、r は電線の抵抗[Ω]とする。
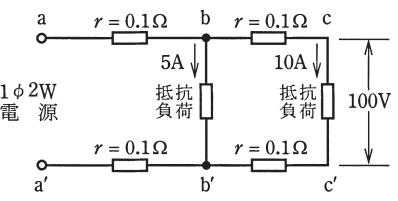
イ. 102 ロ. 103 ハ. 104 二. 105
b-b’ 間の電圧を $V_b$[V]、電圧降下を $v_b$[V]とすると、
$v_b=V_b-V_c=V_b-100$[V]
$v_b=2Ir=2×10×0.1=2$[V]
∴$V_b=102$[V]
a-a’ 間の電圧を $V_a$[V]、電圧降下を $v_a$[V]とすると、
$v_a=V_a-V_b=V_a-102$[V]
$v_a=2Ir=2×(10+5)×0.1=3$[V]
∴$V_a=105$[V]
答え(二)
2009年(平成21年)問6
2011年(平成23年)上期 問7
2013年(平成25年)上期 問6 類似
2019年(令和元年)上期 問6
問6 単相3線式回路の電圧降下と電力損失①
図のような単相 3 線式回路で、電線1線当たりの抵抗 r[Ω]、負荷電流が I[A]、中性点に流れる電流が 0[A]のとき、電圧降下 ( Vs – Vr )[V]を示す式は。
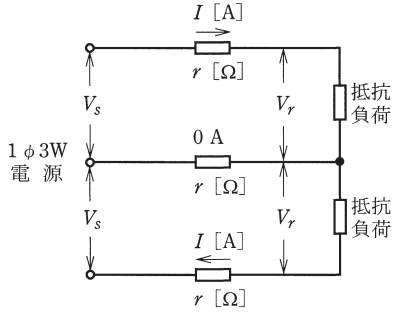
イ. rI ロ. 1.73rI ハ. 2rI 二. 3rI
中性線には電流が流れませんので、外側 1線分の電圧降下を考えればいいので、
Vs – Vr =rI[V]
答え(イ)
2014年(平成26年)下期 問6
2019年(令和元年)上期 問7
問7 単相3線式回路の電圧降下と電力損失②
図のような単相3線式回路において、電線1線当たりの電気抵抗が 0.1[Ω]、抵抗負荷に流れる電流がともに 20[A]〔A〕のとき、この電線路の電力損失[W]は。
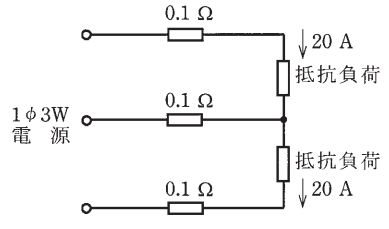
イ. 40 ロ. 69 ハ. 80 二. 120
抵抗負荷に流れる電流が両方共 20A ですので、負荷は平衡しています。この場合、中性線には電流が流れません。したがって、外側 2線の電線の抵抗 $r$ による電力損失 $P_L$[W]を考えればいいので、
$P_L = 2I^2r =2×20^2×0.1=80$[W]
答え(ハ)
2007年(平成19年)問7 類似
2012年(平成24年)上期 問8 類似
2015年(平成27年)下期 問7
問8 単相3線式回路の電圧降下と電力損失③
図のような単相3線式回路において、電線1線当たりの電気抵抗が 0.1[Ω]のとき、a-b 間の電圧[V]は。
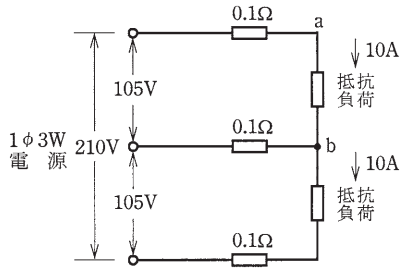
イ. 102 ロ. 103 ハ. 104 二. 105
抵抗負荷に流れる電流が両方共 10A ですので、負荷は平衡しています。この場合、中性線には電流が流れません。したがって、上側の電線の 1線分の電圧降下を考えればいいので、電圧降下を $v$[V] 、a-b 間の電圧 $V_{ab}$[V]とすると、
$v=Ir=10×0.1=1$
$v=Vs-V_{ab}=105-V_{ab}$
∴$V_{ab}=105-v=104$[V]
答え(ハ)
2008年(平成20年)問6 類似
2013年(平成25年)下期 問6
2016年(平成28年)上期 問6 類題
2018年(平成30年)上期 問7 類題
2018年(平成30年)下期 問7
問9 単相3線式回路の電圧降下と電力損失④
図のような単相3線式回路において、電線1線当たりの電気抵抗が 0.1[Ω]のとき、a-b 間の電圧[V]は。
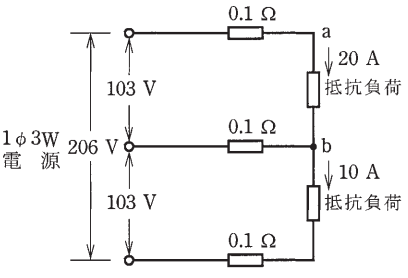
イ. 99 ロ. 100 ハ. 101 二. 102
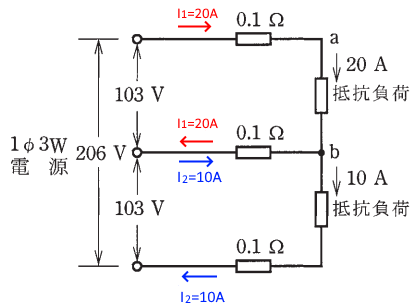
負荷抵抗に流れる電流が異なりますので、中性線には 20-10=10[A]の電流が流れます。電圧降下を $v$[V] 、a-b 間の電圧 $V_{ab}$[V]とすると、
$v=I_1r+(I_1-I_2)r=20×0.1+(20-10)×0.1=3$
$v=Vs-V_{ab}=103-V_{ab}$
∴$V_{ab}=103-v=100$[V]
答え(ロ)
2016年(平成28年)下期 問6
問10 単相3線式回路の電圧降下と電力損失⑤
図のような単相3線式回路で、電線1線当たりの抵抗が 0.1[Ω]、負荷に流れる電流がいずれも 10[A]のとき、この電線路の電力損失[W]は。
ただし、負荷は抵抗負荷とする。
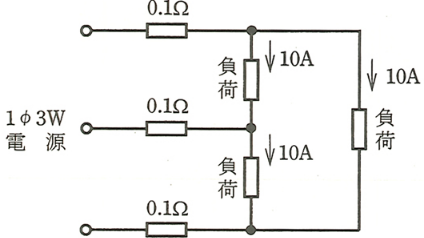
イ. 30 ロ. 80 ハ. 120 二. 160
単相3線式部分の回路で、抵抗負荷に流れる電流が両方共 10A ですので、負荷は平衡しています。この場合、中性線には電流が流れません。したがって、外側 2線の電線の抵抗 $r$ による電力損失 $P_L$[W]を考えます。
外側 2線には、回路図から読み取ると、20A の電流が流れていますので、
$P_L=2I^2r=2×20^2×0.1=80$[W]
答え(ロ)
2011年(平成23年)下期 問7
問11 三相交流回路の電圧降下と電力損失①
図のような三相交流回路において、電線1線当たりの抵抗が r[Ω]、線電流が I[A]であるとき、電圧降下(V1-V2)[V]を示す式は。
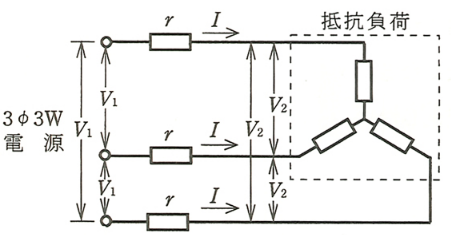
イ. $rI$ ロ. $\sqrt{3}rI$ ハ. $2rI$ 二. $2\sqrt{3}rI$
1相当たりの回路図を示します。
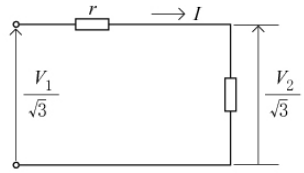
電源の相電圧は $\displaystyle\frac{V_1}{\sqrt{3}}$、負荷の相電圧は $\displaystyle\frac{V_2}{\sqrt{3}}$ ですので、
$\displaystyle\frac{V_1}{\sqrt{3}}-\displaystyle\frac{V_2}{\sqrt{3}}=rI$
$V_1-V_2=\sqrt{3}rI$
答え(ロ)
2006年(平成18年)問7
2011年(平成23年)下期 問8
問12 三相交流回路の電圧降下と電力損失②
図のような三相3線式回路で,電線1線当たりの抵抗が 0.15[Ω]、線電流が 10[A]のとき、電圧降下 ( Vs – Vr )[V]は。
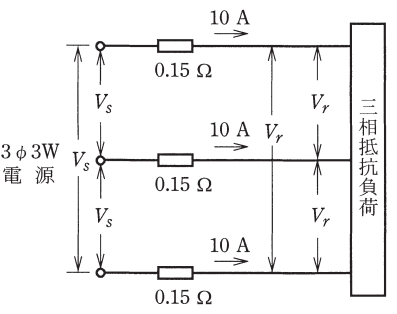
イ. 1.5 ロ. 2.6 ハ. 3.0 二. 4.5
三相3線式回路の電圧降下を $v$[V]は、
$v=Vs-Vr=\sqrt{3}Ir$
$v=1.73×10×0.15≒2.6$[V]
答え(ロ)
2014年(平成26年)上期 問6
2019年(令和元年)下期 問7
問13 三相交流回路の電圧降下と電力損失③
図のような三相3線式回路において、電線1線当たりの電気抵抗が r[Ω]、線電流が I[A]のとき、配線の電力損失[W]を示す式は。
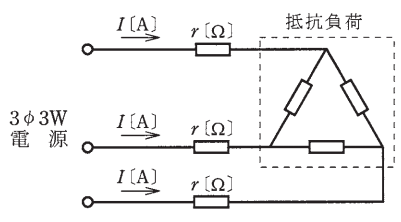
イ. $\sqrt{3}Ir^2$ ロ. $\sqrt{3}I^2r$ ハ. $3Ir^2$ 二. $3I^2r$
三相3線式回路では、3線分の電力損失を考えますので $P_L$[W]は、
$P_L = 3I^2r $
答え(二)
2008年(平成20年)問7
2013年(平成25年)下期 問7
問14 三相交流回路の電圧降下と電力損失④
図のような三相 3 線式回路で、電線 1 線当たりの抵抗値が 0.15 Ω 、線電流が 10 A のとき、この電線路の電力損失[W]は。
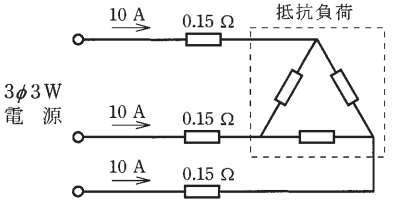
イ. 2.6 ロ. 15 ハ. 26 二. 45
三相3線式回路の電力損失 $P_L$[W]は、
$P_L = 3I^2r =3×10^2×0.15=45$[W]
答え(二)
2011年(平成23年)上期 問8 類似
2016年(平成28年)下期 問8
問15 三相交流回路の電圧降下と電力損失⑤
図のような三相3線式回路で、線電流が 10[A]のとき、この電線路の電力損失[W]は。ただし、電線 1 線の抵抗は 1[m]当たり 0.01[Ω]とする。
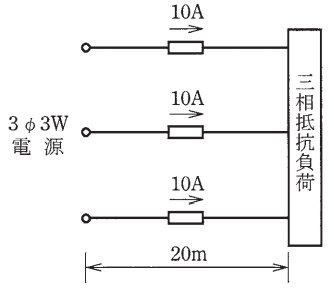
イ. 20 ロ. 35 ハ. 40 二. 60
電線 1本分の抵抗 $r$[Ω]は、
$r=20×0.01=0.2$[Ω]
三相3線式回路の電力損失 $P_L$[W]は、
$P_L = 3I^2r =3×10^2×0.2=60 $[W]
答え(二)
2014年(平成26年)下期 問7
2015年(平成27年)上期 問6 類題
問16 電線の太さ
図のような単相2線式配線において、抵抗負荷に 10 [A] の電流が流れたとき、線路の電圧降下を1 [V] 以下にするための電線の太さの最小値 [mm²] は。ただし、電線の抵抗は、断面積 1 [mm²] 、長さ 1 [m] 当たり 0.02 [Ω] とする。
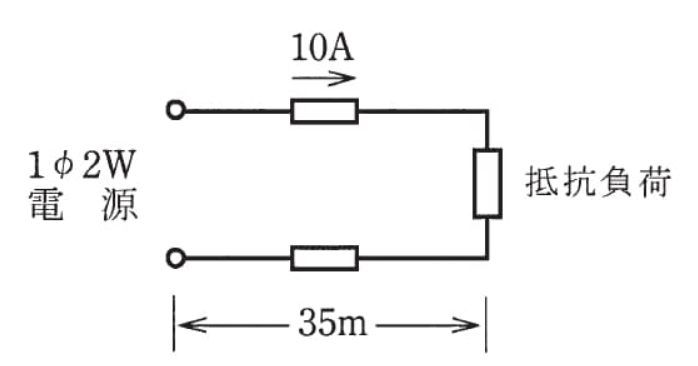
イ. 5.5 ロ. 8 ハ. 14 二. 22
電線の抵抗は、断面積 1 [mm²] 、長さ 1 [m] 当たり 0.02 [Ω] ですので、電線1本あたりの抵抗は、0.02×35=0.7[Ω]
この電線が、2本ありますので、全体として、1.4Ωとなります。
この2本にかかる電圧降下を1Vまで下げる場合、この電線1本あたりにかかる電圧降下を0.5Vまで下げればよいので、
1本の場合:電圧降下[V]=10[A]×0.7[Ω]=7[V]
ここで算出した 7 [V] を 0.5 [V] まで下げるには、7/0.5=14倍 の太さの電線が必要になります。
したがって、「ハ」が正解となります。
答え(ハ)
2012年(平成24年)上期 問7



