第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の機械科目に出題される「変圧器の電圧変動率」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の機械科目の試験で、実際に出題された「変圧器の電圧変動率」の過去問題も解説しています。
変圧器の定格
変圧器の定格とは、指定された電圧、周波数における使用限度を表したものです。変圧器の銘板には、定格として電圧・電流・周波数・力率・容量などの値が示されています。定格容量は、銘板に記載された皮相電力で表されます。これは、二次定格電圧・定格周波数および定格力率において、指定された温度上昇の限度を超えない状態で、二次側で得られる容量であり、[kV・A]の単位で表されます。
定格容量と電圧、電流の関係式
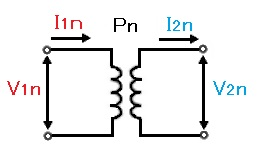
Pn = V1n × I1n = V2n × I2n
Pn:定格容量
V1n:定格一次電圧
I1n:定格一次電流
V2n:定格二次電圧
I2n:定格二次電流
電圧変動率
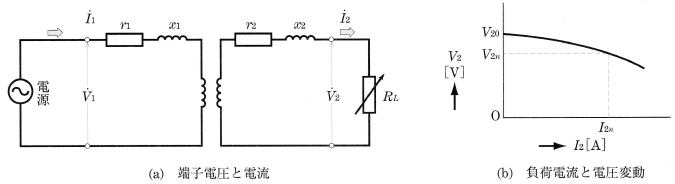
図1(a)に示すように、変圧器の二次側に負荷をつなぎ、一次側に電圧を加えて、負荷抵抗 $R_L$[Ω]をしだいに小さくすると、図(b)に示すように、負荷電流 $I_2$[A]が増加するとともに、二次端子電圧 $V_2$[V]は低下します。これは、一次巻線・二次巻線の抵抗と、漏れリアクタンスによる電圧降下のためです。
図1(b)に示すように、二次端子電圧は負荷によって変化しますが、その変化の程度を表すために、「電圧変動率」が用いられます。
定格の電流・カ率・周波数において、二次巻線の端子電圧を定格値 $V_{2n}$ になるように、一次端子電圧を調整します。次に、このままの状態で変圧器を無負荷にしたときの二次端子電圧を $V_{20}$[V]とすると、電圧変動率 $ε$[%]は次の式で表されます。
電圧変動率を求める式
$ε=\displaystyle\frac{V_{20}-V_{2n}}{V_{2n}}×100$
$ε$[%]:電圧変動率
$V_{20}$[V]:無負荷時の二次電圧
$V_{2n}$[V]:定格二次電圧
(定格負荷を接続した時の二次電圧)
等価回路による電圧変動率の算出
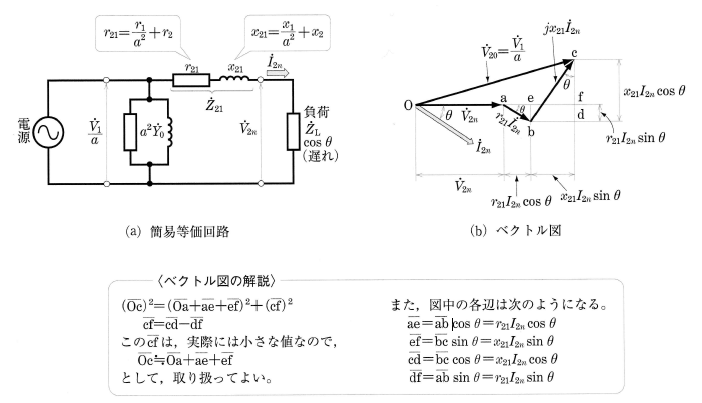
図2(a)は、一次側の諸量を二次側に換算した変圧器の簡易等価回路です。ここで、$r_{21}$[Ω],$x_{21}$[Ω]は、二次側に換算した抵抗および漏れリアクタンスであり、 次の式で表されます。
$r_{21}=\displaystyle\frac{r_1}{a^2}+r_2$
$x_{21}=\displaystyle\frac{x_1}{a^2}+x_2$
また、$\displaystyle\frac{\dot{V}_1}{a}$[V]は、無負荷のときの二次端子電圧 $\dot{V}_{20}$[V]と考えることができ、$\dot{V}_2$[V]は、二次定格電流 $\dot{I}_{2n}$[A]が流れているときの二次端子電圧 $\dot{V}_{2n}$[V]と考えることができます。
この簡易等価回路の電圧・電流のベクトル図を図(b)に示します。$V_{20}$[V]は、このベクトル図から、次の式で表すことができます。
$V_{20}=\sqrt{(V_{2n}+r_{21}I_{2n}cosθ+x_{21}I_{2n}sinθ)^2+(x_{21}I_{2n}cosθ-r_{21}I_{2n}sinθ)^2}$
根号の中の第2項は第1項に比べて非常に小さいので、これを無視すると、次の式が得られます。
$V_{20}=V_{2n}+r_{21}I_{2n}cosθ+x_{21}I_{2n}sinθ$
これから、電圧変動率 $ε$[%]は、次の式で表すことができます。
$ε=\displaystyle\frac{V_{20}-V_{2n}}{V_{2n}}×100$
$=\displaystyle\frac{r_{21}I_{2n}cosθ}{V_{2n}}×100+\displaystyle\frac{x_{21}I_{2n}sinθ}{V_{2n}}×100$
ここで、次に示す $p$[%],$q$[%]を考えます。
$p=\displaystyle\frac{r_{21}I_{2n}}{V_{2n}}×100$
$q=\displaystyle\frac{x_{21}I_{2n}}{V_{2n}}×100$
この式からわかるように、$p$[%],$q$[%]は、定格電流が流れるときの巻線抵抗および漏れリアクタンスによる電圧降下の、定格電圧に対する割合を百分率で示したものです。それぞれを変圧器の「百分率抵抗降下、百分率リアクタンス降下」といい、電圧変動率 $ε$[%]は次の式で表すこともできます。
電圧変動率を求める式
$ε=pcosθ+qsinθ$
$ε$[%]:電圧変動率
$p$[%]:百分率抵抗降下
$q$[%]:百分率リアクタンス降下
$cosθ$:力率
力率 $cosθ$ が1であれば、$ε=p$ で与えられます。
百分率抵抗降下(パーセント抵抗降下 )
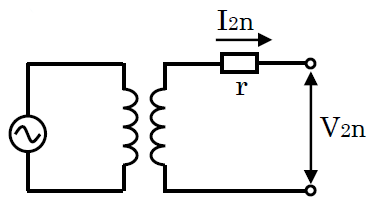
定格二次電圧 と 定格二次電流が流れたときの、巻線抵抗による電圧降下の比率をパーセント表示で表したものです(定格二次電圧に対する 巻線抵抗による電圧降下の割合)。
百分率(パーセント)抵抗降下を求める式
$p=\displaystyle\frac{rI_{2n}}{V_{2n}}×100$
$p$[%]:百分率抵抗降下
$I_{2n}$:定格二次電流
$V_{2n}$:定格二次電圧
$r$:巻線抵抗
百分率リアクタンス降下(パーセントリアクタンス降下)
定格二次電圧と定格二次電流が流れたときの漏れリアクタンスによる電圧降下の比率をパーセント表示で表したものです(定格二次電圧に対する漏れリアクタンスによる電圧降下の割合)。
百分率(パーセント)リアクタンス降下を求める式
$q=\displaystyle\frac{xI_{2n}}{V_{2n}}×100$
$q$[%]:百分率リアクタンス降下
$I_{2n}$:定格二次電流
$V_{2n}$:定格二次電圧
$x$:漏れリアクタンス
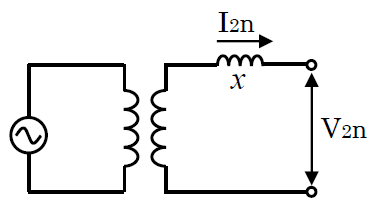
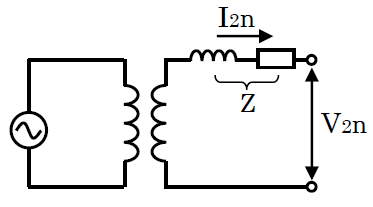
百分率インピーダンス降下(パーセントインピーダンス降下)
定格二次電圧と定格二次電流が流れたときの巻線のインピーダンスによる電圧降下の比率をパーセント表示で表したものです(定格二次電圧 に対する 巻線抵抗による電圧降下の割合)。
百分率(パーセント)インピーダンス降下を求める式
%$Z=\displaystyle\frac{zI_{2n}}{V_{2n}}×100$
%$Z$[%]:百分率インピーダンス降下
$I_{2n}$:定格二次電流
$V_{2n}$:定格二次電圧
$z$:巻線抵抗と漏れリアクタンスの合成インピーダンス
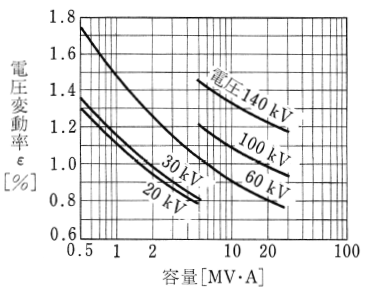
電圧変動率の値
図3は、単相油入変圧器の容量[MV・A]と電圧変動率 $ε$[%]の関係を調べたものです。一般に、容量の大きな変圧器ほど電圧変動率は小さくなります。
インピーダンス電圧
図4(a)に示すように、低圧側を短絡して電圧を加え、そのときの電流 $\dot{I}_{1S}$[A]が定格一次電流 $\dot{I}_{1n}$[A]に等しいとき、その供給電圧 $\dot{V}_{1Z}$[V]をインピーダンス電圧といいます。
図(b)は、図(a)の二次側を一次側に換算した等価回路です。また、図(c)はそのベクトル図です。$\dot{V}_{1Z}$ は、図(c)のベクトル図に示すように、$r_{12}\dot{I}_{1n}+jx_{12}\dot{I}_{1n}$ であり、定格電流が流れているときの、巻線のインピーダンスによる電圧降下を表しています。
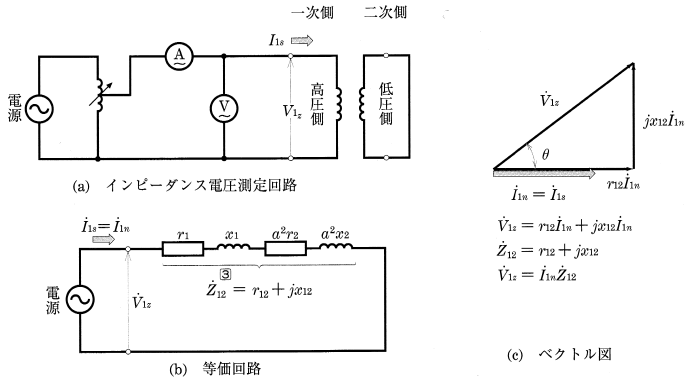
インピーダンス電圧 $V_{1Z}$[V]と定格電圧 $V_{1n}$[V]の比 $z$[%]は、百分率インピーダンス降下とよばれ、次の式で表すことができます。
$\begin{eqnarray}z&=&\displaystyle\frac{V_{1Z}}{V_{1n}}×100=\displaystyle\frac{I_{1n}Z_{12}}{V_{1n}}×100\\&=&\sqrt{\left(\displaystyle\frac{r_{12}I_{1n}}{V_{1n}}\right)^2+ \left( \displaystyle\frac{x_{12}I_{1n}}{V_{1n}}\right)^2}×100\\&=&\sqrt{p^2+q^2} \end{eqnarray}$
p 、q 、%Z の関係を表す式
%$Z^2=p^2+q^2$
%$Z$[%]:百分率インピーダンス降下
$p$[%]:百分率抵抗降下
$q$[%]:百分率リアクタンス降下
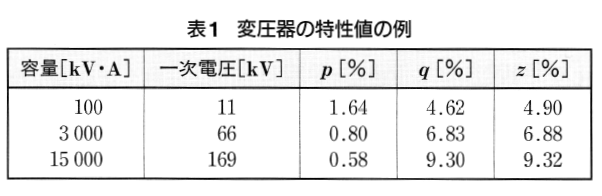
一般に、電圧変動率 $ε$[%]を小さくするには、百分率インピーダンス降下 $z$[%]を小さくする必要があります。しかし、大容量の変圧器では、二次側の短絡事故による過大な短絡電流を防ぐため、百分率インピーダンス降下 $z$[%]をある程度大きくしています。表1はその例です。
短絡電流
電力用の変圧器の銘板には、すべて百分率インピーダンス降下が示されています。すべての電力機器・設備をこの方法で表すことによって、系統に短絡などの事故が発生したとき、各系統の電流を容易に計算することができます。
一次定格電圧 $V_{1n}$ の変圧器の百分率インピーダンス降下が $z$[%]であるとき、短絡電流(一次側)$I_S$[A]は、$I_S=\displaystyle\frac{V_{1n}}{Z_{12}}$ と $Z_{12}=\displaystyle\frac{zV_{1n}}{100I_{1n}}$ により、次の式で表すことができます。
$I_S=\displaystyle\frac{100I_{1n}}{z}$
電験三種-機械の過去問解説:変圧器の電圧変動率
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の機械科目で出題された問題です。
1998年(平成10年)問10
定格二次電圧 200[V]、定格二次電流 100[A]の単相変圧器があり、二次側に換算した全巻線抵抗は 0.03[Ω]、二次側に換算した全漏れリアクタンスは 0.05[Ω]である。この変圧器の力率 0.8(遅れ)における電圧変動率[%]の値として、正しいのは次のうちどれか。
(1) 2.4 (2) 2.7 (3) 3.2 (4) 4.0 (5) 5.1
1998年(平成10年)問10 過去問解説
定格二次電流を $I_{2n}$[A]、定格二次電圧を $V_{2n}$[V]、二次側に換算した巻線抵抗を $r_{21}$[Ω]、二次側に換算した漏れリアクタンスを $x_{21}$[Ω]、変圧器の百分率抵抗降下を $p$[%]、百分率リアクタンス降下を $q$[%]とすると、
$p=\displaystyle\frac{r_{21}I_{2n}}{V_{2n}}×100=\displaystyle\frac{0.03×100}{200}×100=1.5$[%]
$q=\displaystyle\frac{x_{21}I_{2n}}{V_{2n}}×100=\displaystyle\frac{0.05×100}{200}×100=2.5$[%]
力率 0.8(遅れ)における電圧変動率 $ε$[%]は、
$ε=pcosθ+qsinθ=1.5×0.8+2.5×0.6=2.7$[%]
$sinθ=\sqrt{(1-cos²θ)}$
答え (2)
2001年(平成13年)問5
変圧器があり、負荷の力率が1のときの電圧変動率は 2.4[%]であり、負荷の力率が零(遅れ)のときの電圧変動率は 3.2[%]である。負荷の力率が0.8(遅れ)のときの電圧変動率[%]の値として、最も近いのは次のうちどれか。
(1) 2.6 (2) 3.2 (3) 3.8 (4) 4.5 (5) 5.6
2001年(平成13年)問5 過去問解説
変圧器の百分率抵抗降下を $p$[%]、百分率リアクタンス降下を $q$[%]、電圧変動率を $ε$[%]とすると、
$ε=pcosθ+qsinθ$[%]
負荷の力率が1のときの電圧変動率は 2.4[%]なので、
$ε=pcosθ+qsinθ$
$2.4=p×1+q×0$
$p=2.4$[%]
負荷の力率が0のときの電圧変動率は 3.2[%]なので、
$ε=pcosθ+qsinθ$
$3.2=p×0+q×1$
$q=3.2$[%]
したがって、力率0.8(遅れ)における電圧変動率 $ε$[%]は、
$ε=pcosθ+qsinθ=2.4×0.8+3.2×0.6≒3.8$[%]
答え (3)
2005年(平成17年)問16
定格容量500[kV・A]の単相変圧器について、次の(a)及び(b)に答えよ。
(a) 定格時の銅損は 7[kW]であった。この変圧器の百分率抵抗降下 $p$[%]の値として、正しいものは次のうちどれか。
(1) 1.38 (2) 1.40 (3) 1.42 (4) 2.42 (5) 4.20
(b) 定格時において、負荷の力率が $cosθ=0.6$ のとき、電圧変動率 $ε=4$[%]であった。この変圧器の百分率インピーダンス降下 $z$[%]の値として、最も近いのは次のうちどれか。
ただし、百分率リアクタンス降下を $q$[%]とするとき、$ε= pcosθ + qsinθ$ の近似式が成り立つものとする。
(1) 4.00 (2) 4.19 (3) 4.59 (4) 5.35 (5) 5.45
2005年(平成17年)問16 過去問解説
(a) 定格容量を $P_n$[kV・A]、定格二次電流を $I_{2n}$[A]、定格二次電圧を $V_{2n}$[V]、二次側に換算した巻線抵抗を $r_{21}$[Ω]、変圧器の百分率抵抗降下 $p$[%]は、
$p=\displaystyle\frac{r_{21}I_{2n}}{V_{2n}}×100=\displaystyle\frac{r_{21}{I_{2n}}^2}{V_{2n}I_{2n}}×100=\displaystyle\frac{r_{21}{I_{2n}}^2}{P_n}×100$
$r_{21}{I_{2n}}^2$ は、巻線に流れる電流によるジュール熱を表し、銅損(抵抗損)と呼ばれます。したがって、
$p=\displaystyle\frac{r_{21}{I_{2n}}^2}{P_n}×100=\displaystyle\frac{7}{500}×100≒1.40$[%]
答え (2)
(b) 負荷の力率が $cosθ=0.6$ のとき、電圧変動率が $ε=4$[%]$ですので、
$ε= pcosθ+qsinθ$
$4= 1.4×0.6+q×0.8$
$q=3.95$
百分率インピーダンス降下 $z$[%]は、
$z=\sqrt{p^2+q^2}=\sqrt{1.4^2+3.95^2}≒4.19$[%]
答え (2)
2011年(平成23年)問15
次の定数をもつ定格一次電圧 2000[V]、定格二次電圧 100[V]、定格二次電流 1000[A]の単相変圧器について、(a)及び(b)の問に答えよ。
ただし、励磁アドミタンスは無視するものとする。
一次巻線抵抗 $r_1=0.2$[Ω]、一次漏れリアクタンス $x_1=0.6$[Ω]
二次巻線抵抗 $r_2=0.0005$[Ω]、二次漏れリアクタンス $x_2=0.0015$[Ω]
(a) この変圧器の百分率インピーダンス降下[Ω]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 2.00 (2) 3.16 (3) 4.00 (4) 33.2 (5) 664
(b) この変圧器の二次側に力率 0.8(遅れ)の定格負荷を接続して運転しているときの電圧変動率[%]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 2.60 (2) 3.00 (3) 27.3 (4) 31.5 (5) 521
2011年(平成23年)問15 過去問解説
(a) 二次側に換算した巻線抵抗を $r_{21}$[Ω]、二次側に換算した漏れリアクタンスを $x_{21}$[Ω]とすると、
$r_{21}=\displaystyle\frac{r_1}{a^2}+r_2=\displaystyle\frac{0.2}{(\displaystyle\frac{2000}{100})^2}+0.0005=0.001$
$x_{21}=\displaystyle\frac{x_1}{a^2}+x_2=\displaystyle\frac{0.6}{(\displaystyle\frac{2000}{100})^2}+0.0015=0.003$
変圧器の百分率抵抗降下を $p$[%]、百分率リアクタンス降下を $q$[%]とすると、
$p=\displaystyle\frac{r_{21}I_{2n}}{V_{2n}}×100=\displaystyle\frac{0.001×1000}{100}×100=1$
$q=\displaystyle\frac{x_{21}I_{2n}}{V_{2n}}×100=\displaystyle\frac{0.003×1000}{100}×100=3$[%]
百分率インピーダンス降下 $z$[%]は、
$z=\sqrt{p^2+q^2}=\sqrt{1^2+3^2}≒3.16$[%]
答え (2)
(b) 力率0.8(遅れ)における電圧変動率 $ε$[%]は、
$ε=pcosθ+qsinθ=1×0.8+3×0.6=2.60$[%]
答え (1)
2012年(平成24年)問7
単相変圧器があり、二次側を開放して電流を流さない場合の二次電圧の大きさを 100[%]とする。二次側にリアクトルを接続して力率 0 の電流を流した場合、二次電圧は 5[%]下がって 95[%]であった。二次側に抵抗器を接続して、前述と同じ大きさの力率 1 の電流を流した場合、二次電圧は 2[%]下がって 98[%]であった。一次巻線抵抗と一次換算した二次巻線抵抗との和は 10[Ω]である。鉄損及び励磁電流は小さく、無視できるものとする。ベクトル図を用いた電圧変動率の計算によく用いられる近似計算を利用して、一次漏れリアクタンスと一次換算した二次漏れリアクタンスとの和[Ω]の値を求めた。その値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 5 (2) 10 (3) 15 (4) 20 (5) 25
2012年(平成24年)問7 過去問解説
変圧器の百分率抵抗降下を $p$[%]、百分率リアクタンス降下を $q$[%]、電圧変動率を $ε$[%]とすると、
$ε=pcosθ+qsinθ$[%]
力率 0 の電流を流した場合、二次電圧は 5[%]下がったので、この時の電圧変動率は $ε=5$[%]となり、
$ε=pcosθ+qsinθ$
$5=p×0+q×1$
$q=5$[%]
力率 1 の電流を流した場合、二次電圧は 2[%]下がったので、この時の電圧変動率は $ε=2$[%]となり、
$ε=pcosθ+qsinθ$
$5=p×1+q×0$
$p=2$[%]
定格二次電流を $I_{2n}$[A]、定格二次電圧を $V_{2n}$[V]、二次側に換算した巻線抵抗を $r_{21}$[Ω]、二次側に換算した漏れリアクタンスを $x_{21}$[Ω]とすると、
$p=\displaystyle\frac{r_{21}I_{2n}}{V_{2n}}×100$[%]
$q=\displaystyle\frac{x_{21}I_{2n}}{V_{2n}}×100$[%]
この2式の関係は、$\displaystyle\frac{p}{r_{21}}=\displaystyle\frac{q}{x_{21}}$ となりますので、
$\displaystyle\frac{p}{r_{21}}=\displaystyle\frac{q}{x_{21}}$
$\displaystyle\frac{2}{10}=\displaystyle\frac{5}{x_{21}}$
$x_{21}=25$[Ω]
答え (5)
2014年(平成26年)問8
次の文章は、単相変圧器の電圧変動に関する記述である。
単相変圧器において、一次抵抗及び一次漏れリアクタンスが励磁回路のインピーダンスに比べて十分小さいとして二次側に移した、二次側換算の簡易等価回路は図のようになる。$r_{21}=1.0×10^{-3}$ Ω、$x_21=3.0×10^{-3}$ Ω、定格二次電圧 $V_{2n}=100$ V、定格二次電流 $I_{2n}=1$ kAとする。負荷の力率が遅れ 80 %のとき、百分率抵抗降下 $p$、百分率リアクタンス降下 $q$ 及び電圧変動率 $ε$ のそれぞれの値[%]の組合せとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
なお、本問では簡単のため用いられる近似式を用いて解答すること。
| $p$ | $q$ | $ε$ | |
| (1) | 3.0 | 1.0 | 3.0 |
| (2) | 3.0 | 1.0 | 2.4 |
| (3) | 1.0 | 3.0 | 3.1 |
| (4) | 1.0 | 2.6 | 3.0 |
| (5) | 1.0 | 3.0 | 2.6 |
2014年(平成26年)問8 過去問解説
変圧器の百分率抵抗降下 $p$[%]は、
$p=\displaystyle\frac{r_{21}I_{2n}}{V_{2n}}×100=\displaystyle\frac{1.0×10^{-3}×1000}{100}×100=1.0$
百分率リアクタンス降下 $q$[%]は、
$q=\displaystyle\frac{x_{21}I_{2n}}{V_{2n}}×100=\displaystyle\frac{3.0×10^{-3}×1000}{100}×100=3.0$[%]
力率0.8(遅れ)における電圧変動率 $ε$[%]は、
$ε=pcosθ+qsinθ=1.0×0.8+3.0×0.6=2.6$[%]
答え (5)






