電験三種の法規で出題される変圧器の損失と効率について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の試験で、実際に出題された過去問題も解説しています。
変圧器の損失
変圧器の損失には、鉄損と銅損があります。鉄損は、鉄心中の磁束に変化による損失で、変圧器の負荷の大きさに関係なく一定です。銅損は、1次巻線と2次巻線の抵抗による損失で、電流の2乗に比例します。
力率 100%で、変圧器の鉄損を Pi[kW]、定格負荷時の銅損 Pc[kW]とし、24時間定格運転する変圧器の一日中の鉄損電力量 Wi[kWh]と銅損電力量 Wc[kWh]は、
Wi=Pi×24[kWh]
Wc=Pc×24[kWh]
また、変圧器の損失電力量は W[kWh]は、一日中の鉄損電力量 Wi[kWh]と銅損電力量 Wc[kWh]の合計になります。
W=Wi+Wc[kWh]
変圧器の効率
変圧器の効率 η[%]は、出力と入力との比の百分率で定義されます。冷却設備の損失などは除外されますが、標準として各損失を測定し、次の規約効率により算出します。
$η=\displaystyle \frac{ 出力 }{ 出力+損失 }×100$
また、変圧器の1日の平均的な効率として、全日効率 $η_d$[%]が定義されています。
$η_d=\displaystyle \frac{ W_d }{W_d+W }×100$
Wd[kWh]:一日中に出力する電力量
W[kWh]:変圧器の損失電力量
その他の公式
$日負荷率=\displaystyle \frac{ 平均負荷 }{最大負荷 }×100$
$過負荷率=\displaystyle \frac{ (負荷 – 設備容量) }{ 設備容量 }×100$
電験三種-法規(施設管理)過去問題
1998年(平成10年)問11
定格容量 10[kV・A]、定格二次電流 100[A]、定格負荷時の銅損 330[W]、定格電圧時の鉄損 120[W]の単相変圧器がある。この変圧器の二次側の日負荷曲線が図のような場合、1日の損失電力量[kWh]の値として、正しいのは次のうちどれか。ただし、負荷の力率は 100[%]とする。
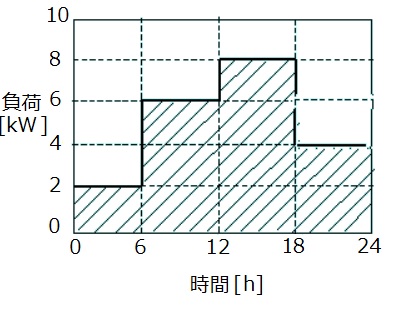
(1) 3.6 (2) 5.3 (3) 7.6 (4) 8.8 (5) 10.8
1998年(平成10年)問11 過去問解説
変圧器の鉄損は、負荷の有無にかかわらず一定です。銅損は、負荷率の2乗に比例して増減します。 一日中の鉄損電力量を $ W_i$[kWh]、銅損電力量 $W_c$[kWh]とすると、題意より
$ W_i=0.12×24=2.88[kWh]$
$\begin{eqnarray}W_c &=& \left[\left( \frac{ 2 }{ 10 }\right)^2×6+\left(\frac{ 6 }{ 10 }\right)^2×6+\left(\frac{ 8}{ 10 }\right)^2×6+\left( \frac{ 4 }{ 10 }\right)^2×6\right]×0.33 \\\\ &=& (0.04+0.36+0.64+0.16)×6×0.33 \\\\ &≒&2.38[kWh]\end{eqnarray}$
損失電力量 $W$[kWh]は、一日中の鉄損電力量と銅損電力量の合計ですので、
$W=W_i+W_c=5.26[kWh]$
答え (2)
2001年(平成13年)問12
負荷設備の合計容量 400[kW]、最大負荷電力 250[kW]、遅れ力率 0.8 の三相平衡の動力負荷に対して、定格容量 150[kV・A]の単相変圧器3台をΔ-Δ結線して供給している高圧自家用需要家がある。この需要家について、次の(a)及び(b)に答えよ。
(a) 動力負荷の需要率[%]の値として、正しいのは次のうちどれか。
(1) 50.0 (2) 55.2 (3) 62.5 (4) 78.1 (5) 83.3
(b) いま、3台の変圧器のうち1台が故障したため、2台の変圧器をV結線して供給することとしたが、負荷を抑制しないで運転した場合、最大負荷時で変圧器は何パーセント[%]の過負荷となるか。正しい値を次のうちから選べ。
(1) 4.2 (2) 8.3 (3) 14.0 (4) 20.3 (5) 28.0
2001年(平成13年)問12 過去問解説
(a) 需要率は、最大需要電力と設備容量の合計との比のことです。題意より、
$ \begin{eqnarray}需要率&=&\displaystyle \frac{ 最大需要電力 }{ 設備容量の合計 }×100\\\\&=&\displaystyle \frac{ 250 }{ 400 }×100\\\\&=&62.5[%]\end{eqnarray}$
答え (3)
(b) $S$[kV・A]の2台の単相変圧器をV結線としたときの三相出力 $W$[kV・A]は、
$W=\sqrt{3}S=\displaystyle \frac{ 250}{ 0.8 }$
$S=\displaystyle \frac{ 250}{ 0.8\sqrt{3} }=180.43$
$過負荷率=\displaystyle \frac{ (負荷 – 設備容量) }{ 設備容量 }×100$ですので、
$過負荷率=\displaystyle \frac{ (180.43 – 150) }{150 }×100=20.28$[%]
答え (4)
2002年(平成14年)問11
定格容量 100[kV・A]、鉄損 900[W]及び全負荷銅損 1.2[kW]の変圧器がある。この変圧器を1日のうち無負荷で 10時間、定格電流 50[%](力率 1.0)で6時間、定格電流(力率 0.85)で 8時間使用するときに、次の(a)及び(b)に答よ。
(a) この変圧器の1日の全損失電力量[KW・h]の値として、正しいのは次のうちどれか。
(1) 80 (2) 66 (3) 55 (4) 46 (5) 33
(b) このときの全日効率[%]の値として、最も近いものは次のうちどれか。
(1) 60.5 (2) 75.2 (3) 80.5 (4) 96.7 (5) 99.3
2002年(平成14年)問11 過去問解説
(a) 変圧器の鉄損は、負荷の有無にかかわらず一定です。銅損は、負荷率の2乗に比例して増減します。 一日中の鉄損電力量を $W_i$[kWh]、銅損電力量 $W_c$[kWh]とすると、題意より
$ W_i=0.9×24=21.6$[kWh]
$W_c = 1.2×(0.5^2×6+1^2×8)=11.4$[kWh]
損失電力量 $W$[kWh]は、一日中の鉄損電力量と銅損電力量の合計ですので、
$W=W_i+W_c=33.0$[kWh]
答え (5)
(b) この変圧器の一日中に出力する電力量 $W_d$[kWh]は、
$W_d=100×0.5×6+100×0.85×8=980$[kWh]
したがって全日効率 $η_d$ は、
$η_d=\displaystyle \frac{ W_d }{W_d+W }×100=\displaystyle \frac{ 980 }{980+33 }×100=96.7$
答え (4)
2007年(平成19年)問12
配電線路に接続された、定格容量 20[kV・A]、定格二次電流 200[A]、定格電圧時の鉄損 150[W]、定格負荷時の銅損 270[W]の単相変圧器がある。この変圧器の二次側の日負荷曲線が図のような場合について、次の(a)及び(b)に答えよ。
ただし、負荷の力率は 100[%]とする。
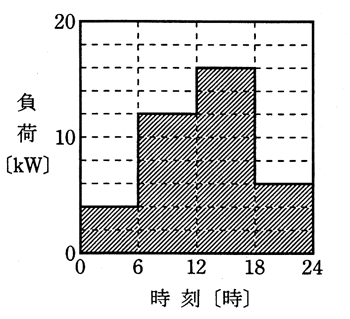
(a) 変圧器の1日の損失電力量[kWh]の値として、最も近いのは次のうちどれか。
(1) 3.68 (2) 3.91 (3) 5.43 (4) 7.00 (5) 7.50
(b) 変圧器の全日効率[%]の値として、最も近いのは次のうちどれか。
(1) 96.8 (2) 97.0 (3) 97.7 (4) 98.4 (5) 99.0
2007年(平成19年)問12 過去問解説
(a) 変圧器の鉄損は、負荷の有無にかかわらず一定です。銅損は、負荷率の 2乗に比例して増減します。 一日中の鉄損電力量を $W_i$[kWh]、銅損電力量 $W_c$[kWh]とすると、題意より
$ W_i=0.15×24=3.6$[kWh]
$\begin{eqnarray}W_c &=& \left[\left(\displaystyle \frac{ 4 }{ 20 }\right)^2×6+\left(\displaystyle \frac{ 12 }{ 20 }\right)^2×6+\left(\displaystyle \frac{ 16}{ 20 }\right)^2×6+\left(\displaystyle \frac{ 6}{ 20 }\right)^2×6\right]×0.27 \\\\ &=& (0.04+0.36+0.64+0.09)×6×0.27 \\\\ &≒&1.83 [kWh]\end{eqnarray}$
損失電力量 $W$[kWh]は、一日中の鉄損電力量と銅損電力量の合計ですので、
$W=W_i+W_c=5.43$[kWh]
答え (3)
(b) この変圧器の一日中に出力する電力量 $W_d$[kWh]は、
$W_d=4×6+12×6+16×6+6×6=228$[kWh]
したがって全日効率 $η_d$ は、
$η_d=\displaystyle \frac{ W_d }{W_d+W }×100=\displaystyle \frac{ 228 }{228+5.43 }×100=97.7$
答え (3)
2007年(平成19年)問13
負荷設備(低圧のみ)の容量が 600[kW]、需要率が 60[%]の高圧需要家について、次の(a)及び(b)に答えよ。
(a) 下表に示す受電用変圧器バンク容量[kV・A]が選択できる。

この中から、この需要家に設置すべき必要最小限の変圧器バンク容量[kV・A]として選ぶとき、正しいのは次のうちどれか。ただし、負荷設備の総合力率は 0.8 とする。
(1) 375 (2) 400 (3) 500 (4) 550 (5) 600
(b) 年負荷率を 55[%]とするとき、負荷の年間総消費電力量[MW・h]の値として,最も近いのは次のうちどれか。ただし、1年間の日数は365日とする。
(1) 1665 (2) 1684 (3) 1712 (4) 1734 (5) 1754
2007年(平成19年)問13 過去問解説
(a) 最大電力を $P_m$[kW]とすると、
$P_m=600×0.6=360$[kW]
力率が 0.8 なので、変圧器容量を $S$[kV・A]とすると、
$S=\displaystyle \frac{ P_m }{0.8 }=\displaystyle \frac{ 360 }{0.8 }=450$[kV・A]
よって、変圧器の最小バンク容量は 500[kV・A]になります。
答え (3)
(b) 年間の平均電力を $P_a$[kW]とすると、年負荷率は 55[%]なので、
$P_a=P_m×0.55=360×0.55=198$[kW]
負荷の年間総消費電力量を $W$[MW・h]とすると、
$W=P_a×24×365×10^{-3}≒1734$[MW・h]
答え (4)
2011年(平成23年)問11
ある需要家設備において定格容量 30[kV・A]、鉄損 90[W]及び全負荷銅損 550[W]の単相変圧器が設置してある。ある1日の負荷は、
24[kW],力率 80[%]で4時間
15[kW],力率 90[%]で8時間
10[kW],力率 100[%]で6時間
無負荷で6時間
であった。この日の変圧器に関して、次の(a)及び(b)の問に答えよ。
(a) この変圧器の全日効率[%]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 97.4 (2) 97.6 (3) 97.8 (4) 98.0 (5) 98.2
(b) この変圧器の日負荷率[%]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 38 (2) 48 (3) 61 (4) 69 (5) 77
2011年(平成23年)問11 過去問解説
(a) 変圧器の鉄損は、負荷の有無にかかわらず一定です。銅損は、負荷率の2乗に比例して増減します。 一日中の鉄損電力量を $ W_i$[kWh]、銅損電力量 $W_c$[kWh]とすると、題意より
$ W_i=0.09×24=2.16$[kWh]
$\begin{eqnarray}W_c &=& \left[\left(\displaystyle \frac{ \frac{ 24 }{ 0.8 } }{ 30 }\right)^2×4+\left(\displaystyle \frac{ \frac{ 15 }{ 0.9 } }{ 30 }\right)^2×8+\left(\displaystyle \frac{ \frac{ 10 }{ 1 }}{ 30 }\right)^2×6\right]×0.55 \\\\ &=& (4+2.47+0.67)×0.55 \\\\ &≒&3.93 [kWh]\end{eqnarray}$
この変圧器の一日中に出力する電力量 $W_d$[kWh]は
$W_d=24×4+15×8+10×6=276$[kWh]
したがって全日効率 $η_d$ は、
$\begin{eqnarray}η_d&=&\displaystyle \frac{ W_d }{W_d+W_i+W_c }×100\\\\&=&\displaystyle \frac{ 276 }{276+2.16+3.93 }×100\\\\&=&97.8\end{eqnarray}$
答え (3)
(b) $日負荷率=\displaystyle \frac{ 平均負荷 }{最大負荷 }×100$ ですので、
$日負荷率=\displaystyle \frac{ \displaystyle \frac{ 276 }{24 } }{24 }×100=47.9$[%]
答え (2)





