交流電力の有効分と無効分【電気設備】

これだけは知っておきたい電気設備の基礎知識をご紹介します。このページでは「交流電力の有効分と無効分」について、維持管理や保全などを行う電気技術者の方が、知っておくとためになる電気の基礎知識を解説しています。

交流回路の有効分と無効分
1. 有効電力と有効電流
2. 無効電流と無効電力
有効電力、無効電力、皮相電力の計算
三相誘導電動機の銘板の意味
1. 定格電圧と定格電流
2. 定格出力
三相誘導電動機の有効電力と無効電力
1. 定格電圧、定格電流より求める場合
2. 定格出力より求める場合

交流回路の有効分と無効分

交流においては、有効電力や無効電力ということばが使われますが、第1図の回路でこれを調べてみます。

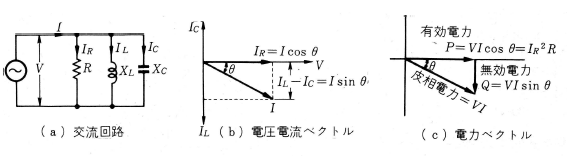
有効電力と有効電流

第1図 (a)において、抵抗 $R$〔Ω〕に流れる電流は、

$I_R=\displaystyle \frac{V}{R}$〔A〕

で、$V$ と同相であり抵抗 $R$ においては $I_R^2R$〔J/s〕の熱が発生し、

$I_R^2R=VI_R$〔W〕

の電力の消費があります。この抵抗 $R$ を流れる電流 $I_R$ のように、電気エネルギーの消費にともなう電流を有効電流といい、

(電圧)×(電圧と同相分の電流) $=VI_R$

を有効電力といいます。これを波形で調べると第2図 (a)のようになり、斜線を施した部分の面積、つまり電力は電圧の実効値と電流の実効値を掛けたもの $VI_R$ に等しくなります。なお、単に電力あるいは消費電力という場合は、この有効電力を指しています。

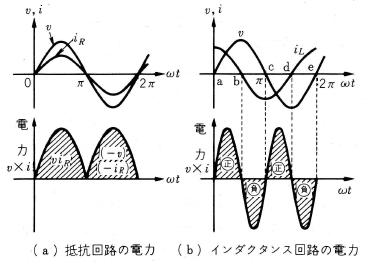
無効電流と無効電力

誘導リアクタンス $X_L$〔Ω〕のコイルに流れる電流 $I_L$ は $\displaystyle \frac{V}{X_L}$〔A〕で、電圧 $V$ より $\displaystyle \frac{π}{2}$ 位相が遅れています。コイルにこの電流 $I_L$ が流れた場合の電力はどうなるか調べてみます。

第2図 (b)において、ab間での電力は $v×i_L$ で +であるから、電源より電力がコイルに供給され、コイルは電磁エネルギーを蓄えます。次にbc間では、 $i_L$ が -であるから $v×i_L$ も-となり、コイルに蓄えた電磁エネルギーを放出し、電力として電源に返されます。

つまり、電源とコイルの間を電気エネルギーが交互に移動するのみで、電力の消費はありません。これと同様に、容量リアクタンス $X_C$〔Ω〕のコンデンサに流れる電流 $I_C$ は $\displaystyle \frac{V}{X_C}$〔A〕で、$V$ より $\displaystyle \frac{π}{2}$ 進んでいますが、コンデンサにこの電流が流れると、ある期間は充電されて電気エネルギーを蓄え、次の期間は放電して蓄えられた電気エネルギーは電源に返され、一周期を平均すると電力は零となります。

このような、$I_L,I_C$ を、電力の消費をともなわないということで、無効電流といい、

(電圧)× (電圧と90°位相差のある電流)=$VI_L$

あるいは $VI_C$ を無効電力といい、単位にバール〔Var〕を用います。

それでは無効電力は必要ないのではと思うかもしれませんが、たとえば三相誘導電動機においては回転磁界を発生するために、コイルが必要であり、コイルがあれば無効電力が存在します。このように、コイルには磁界の発生、コンデンサには充放電作用など、電気的に重要な役割があり、無効電力が必要なのです。また、交流回路には、負荷ばかりでなく、発電機、変圧器、電線に $L,C$ が在存し、無効電力の発生・消費があります。

有効電力、無効電力、皮相電力の計算

第1図の交流回路のベクトル図は(b)のようになりますので、

入力電流：$I=\sqrt{I_R^2+(I_L-I_C)^2}$〔A〕

有効電流：$I_R=Icosθ$〔A〕、$θ=tan^{-1}\displaystyle \frac{I_L-I_C}{I_R}$

無効電流：$I_L-I_C=Isinθ$〔A〕

有効電力=(電圧)×(電圧と同相の電流)$=VIcosθ$ 〔W〕

となり、単相交流回路の有効電力は、(電圧)×(電流)×(力率)で求めることができます。

無効電力=(電圧)×(電圧と90°位相差のある電流)$=VIsinθ$〔Var〕

また、入力電流 $I$ を皮相電流といい、電圧と皮相電流を掛けたものを、見かけの電力という意味で皮相電力
と呼び、単位に〔VA〕を用います。

皮相電力$=VI$〔VA〕
有効電力=皮相電力×力率

として表わされます。

三相誘導電動機の銘板の意味

三相誘導電動機の銘板には、定格電圧 $V$〔V〕、定格電流 $I$〔A〕、定格周波数 $f$〔Hz〕、定格出力 $P$〔kW〕が明示してあります。

定格電圧と定格電流

定格電圧は第3図に示すように、電動機固定子の三相一次巻線端子 $U,V,W$ の各端子間に加わる三相電圧を表わし、三相交流電源より見れば線間電圧に相当します。定格電流は定格出力時の三相入力電流を表わします。定格周波数は同期速度、つまり回転数を規定するものです。

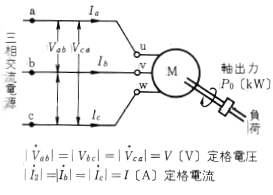
定格出力

定格出力 $P_o$ とは、電動機の軸出力、つまり実際の機械的出力を kW で表わしたものであり、電動機が定格負荷で運転しているときの電動機入力は (定格出力 +損失)となります。電動機損失には、一次固定子巻線、二次回転子導体、巻線の抵抗損、一次巻線磁界により生じるうず電流損、ヒステリシス損などの鉄損、および軸受等の機械損、回転部分の風損などがあり、電動機効率を $η$ とすれば、

電動機入力＝定格出力+損失＝定格出力 /$η$ 〔kW〕

で表わされます。

電動機の効率、力率は銘板に明記されていません。これは、効率、力率はともに電動機出力によって変化し、また、定格電圧、定格出力などのように電動機の仕様を決定するものではないからです。第4図に三相誘導電動機の出力と効率 $η$、力率 $cosθ$ の関係を示します。

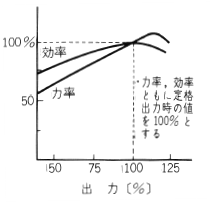
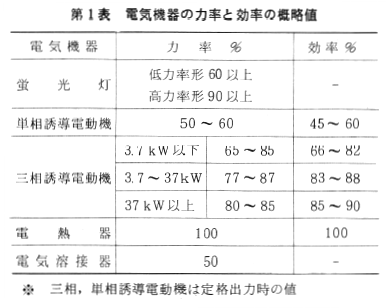
一般に電気使用機器には、効率、力率は明示されていない場合が多いので、電動機、蛍光灯などの代表的機器については、その概略値を知っていると便利ですので、第1表にそれを示します。

三相誘導電動機の有効電力と無効電力

定格電圧 $V=三相 220$〔V〕、定格電流 $I=34$〔A〕、電格出力 $P_o=10$〔kW〕の三相誘導電動機の有効電力、無効電力を次の二つの場合について求めてみます。

(三相交流回路の皮相電力$=\sqrt{3}VI$ , 有効電力$=\sqrt{3}VIcosθ$ , 無効電力$=\sqrt{3}VIsinθ$ で表わされる、次項の単相、三相電力の測定の項を参照)。

定格電圧、定格電流より求める場合

電動機の力率 $cosθ$ を遅れの 85% と仮定すると、

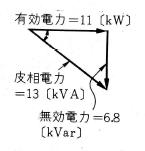
皮相電力$=\sqrt{3}VI=\sqrt{3}×220×34≒13$〔kVA〕
有効電力$=消費電力=\sqrt{3}VIcosθ=13×0.85=11$〔kW〕
遅れ無効電力$=\sqrt{3}VIsinθ=13×0.527≒ 6.8$〔kVar〕
($sinθ=\sqrt{1-(cosθ)^2}=\sqrt{1-(0.85)^2}≒ 0.527$)

ベクトル図を示すと、第5図のようになります。