このページでは、発振回路と変調回路の原理について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の理論科目で、実際に出題された発振回路と変調回路の過去問題の解き方も解説しています。
発信回路
一定の振幅を持つ信号が一定の周波数で連続的に発生する現象を発信といいます。発信回路は、無線通信機器の高周波電波やデジタル時計の基準信号、コンピューターの動作クロックなどをつくるために、多くの電子機器に利用されています。
発振回路の基本は増幅度A、帰還率Fの正帰還増幅回路です。増幅回路の出力信号を入力信号と同相で帰還することで、出力信号を増大させていきます。そして、回路がある条件を満たすと、振幅と周波数が一定の正弦波を得ることができます。
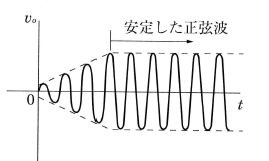
発振の条件は、入力 $v_i$ は増幅回路と帰還回路によって $AF$ 倍に増幅されたのち、再び増幅回路に入力されます。したがって、出力信号を増大させていくためには、回路をループさせた場合にループ利得が $AF>1$ であることが必要です。その後、増幅回路が飽和すると出力信号の振幅は一定になります。回路全体の増幅度 $A_v$ は次の式で表すことができます。
$v_o=v_1A$
$v_1=v_oF+v_i$
$A_v=\displaystyle\frac{v_o}{v_i}=\displaystyle\frac{A}{1-AF}$
$AF=1$ のとき、増幅度 $A_v$ は無限大になります。これは発振を持続することを意味します。
マルチバイブレータ回路
マルチバイブレータ―とは、パルス波形の発生や2値情報の記憶などを行う回路です。マルチバイブレータ―回路の基本は、2段のトランジスタに正帰還をかけた発信回路です。一般的には対称形の表示方法が用いられています。
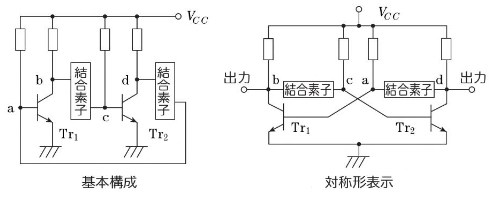
結合素子は抵抗とコンデンサーからなり、その組み合わせによって「非安定マルチバイブレータ」「単安定マルチバイブレータ」「双安定マルチバイブレータ」に分類できます。
| マルチバイブレータの種類 | 結合素子 | 特徴 |
| 非安定 | コンデンサ | 電源を入れると、CとRの時定数で決まる周期で連続してパルスを発生し続けます。 自走マルチバイブレータともいいます。 |
| 単安定 | コンデンサと抵抗 | 入力パルスがあると、その波形に無関係に一定波形を出力します。 ワンショットマルチバイブレータともいいます。 |
| 双安定 | 抵抗 | 入力トリガの2パルスに対して1パルスが出力されます。 カウンタやフリップフロップに利用できます。 |
変調回路
音声や画像信号を無線で送信する場合、伝送したい信号を高周波信号に重ね合わせて送信します。そして、受信側で、受信した電波から目的の信号を分離して取り出します。このように、伝送したい信号を高周波に乗せることを変調、変調波から目的の信号を取り出すことを復調または検波といいます。
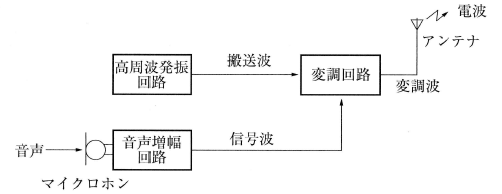
音声信号を電波に乗せて送信する場合、送信したい音声信号を「信号波」、高調波信号のことを「搬送波(キャリア)」といいます。変調回路によって、信号波は搬送波に重ね合わされ、変調波としてアンテナから放射されます。
代表的な変調方式には次のようなものがあります。
- 振幅変調(AM変調)
信号波の振幅に応じて、搬送波の振幅を変化させる方式 - 周波数変調(FM変調)
信号波の振幅に応じて、搬送波の周波数を変化させる方式 - 位相変調(PM変調)
信号波の振幅に応じて、搬送波の位相を変化させる方式
電験三種-理論(電子回路)過去問題
2008年(平成20年)問18
無線通信で行われるアナログ変調・復調に関する記述について、次の(a)及び(b)に答えよ。
(a) 無線通信で音声や画像などの情報を送る場合、送信側においては、情報を電気信号(信号波)に変換する。次に信号波より( ア )周波数の搬送波に信号波を含ませて得られる信号を送信する。受信側では、搬送波と信号波の二つの成分を含むこの信号から( イ )の成分だけを取り出すことによって、音声や画像などの情報を得る。
搬送波に信号波を含ませる操作を変調という。( ウ )の搬送波を用いる基本的な変調方式として、振幅変調(AM)、周波数変調(FM)、位相変調(PM)がある。
搬送波を変調して得られる信号からもとの信号波を取り出す操作を復調又は( エ )という。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる語句として,正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 高い | 信号波 | のこぎり波 | 検波 |
| (2) | 低い | 搬送波 | 正弦波 | 検波 |
| (3) | 高い | 搬送波 | のこぎり波 | 増幅 |
| (4) | 低い | 信号波 | のこぎり波 | 増幅 |
| (5) | 高い | 信号波 | 正弦波 | 検波 |
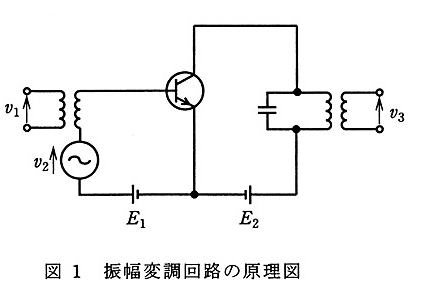
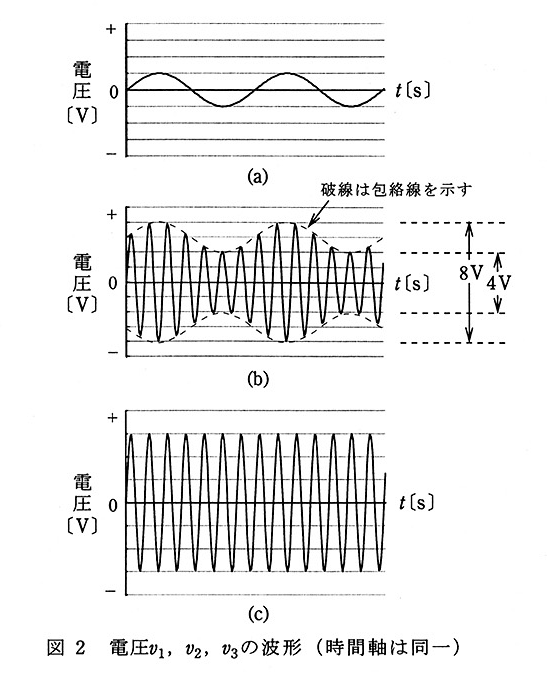
(b) 図1は、トランジスタの( ア )に信号波の電圧を加えて振幅変調を行う回路の原理図である。図1中の $v_2$ が正弦波の信号電圧とすると、電圧 $v_1$ の波形は( イ )に、$v_2$ の波形は( ウ )に、$v_3$ の波形は( エ )に示すようになる。図2のグラフより振幅変調の変調率を計算すると約( オ )[%]となる。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる語句又は数値として、正しいものを組み合わせたのは次のうちどれか。
ただし、図2のそれぞれの電圧波形管の位相関係は無視するものとする。
| (ア) | (イ) | (ウ) | (エ) | (オ) | |
| (1) | ベース | 図2(c) | 図2(a) | 図2(b) | 33 |
| (2) | コレクタ | 図2(c) | 図2(b) | 図2(a) | 67 |
| (3) | ベース | 図2(b) | 図2(a) | 図2(c) | 50 |
| (4) | エミッタ | 図2(b) | 図2(c) | 図2(a) | 67 |
| (5) | コレクタ | 図2(c) | 図2(a) | 図2(b) | 33 |
2008年(平成20年)問18 過去問解説
(a) 信で音声や画像などの情報を送る場合、送信側においては、情報を電気信号(信号波)に変換する。次に信号波より( 高い )周波数の搬送波に信号波を含ませて得られる信号を送信する。受信側では、搬送波と信号波の二つの成分を含むこの信号から( 信号波 )の成分だけを取り出すことによって、音声や画像などの情報を得る。
搬送波に信号波を含ませる操作を変調という。( 正弦波 )の搬送波を用いる基本的な変調方式として、振幅変調(AM)、周波数変調(FM)、位相変調(PM)がある。
搬送波を変調して得られる信号からもとの信号波を取り出す操作を復調又は( 検波 )という。
答え (5)
(b) 図1は、トランジスタの( ベース )に信号波の電圧を加えて振幅変調を行う回路の原理図である。図1中の $v_2$ が正弦波の信号電圧とすると、電圧 $v_1$ の波形は( 図2(c) )に、$v_2$ の波形は( 図2(a) )に、$v_3$ の波形は( 図2(b) )に示すようになる。図2のグラフより振幅変調の変調率を計算すると約( 33 )[%]となる。
変調率は次の式で求めることができます。
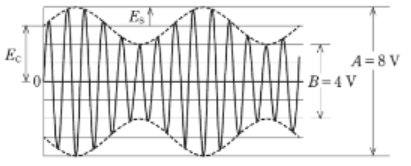
$変調率=\displaystyle\frac{E_S}{E_C}×100=\displaystyle\frac{A-B}{A+B}×100$
答え (1)
2011年(平成23年)問13
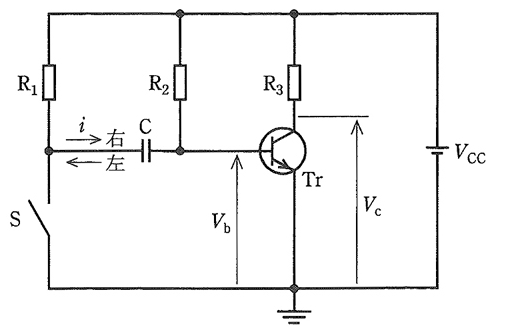
図のように、トランジスタを用いた非安定(無安定)マルチバイブレータ回路の一部分がある。 ここで、Sはトランジスタの代わりの動作をするスイッチ、$R_1$,$R_2$,$R_3$ は抵抗、$C$ はコンデンサ、$V_{CC}$ は直流電源電圧、$V_b$ はベースの電圧、$V_C$ はコレクタの電圧である。
この回路において、初期条件としてコンデンサ $C$ の初期電荷は零、スイッチSは開いている状態と仮定する。
- スイッチS が開いている状態(オフ)のときは、トランジスタ $T_r$ のベースには抵抗 $R_2$ を介して( ア )の電圧が加わるので、トランジスタ $T_R$ は( イ )となっている。 ベースの電圧 $V_b$ は電源電圧 $V_{CC}$ より低いので、電流 $i$ は図の矢印 “右” の向きに流れてコンデンサ $C$ は充電されている。
- 次に、スイッチS を閉じる(オン)と、その瞬間はコンデンサ $C$ に充電されていた電荷でベースの電圧は負となるので、コレクタの電圧 $V_C$ は瞬時に高くなる。
電流 $i$ は矢印 “( ウ )” の向きに流れ、コンデンサ $C$ は( エ )を始め、やがてベースの電圧は( オ )に変化し、コレクタの電圧 $V_C$ は下がる。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして、 正しいものを次の(1) ~ (5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | (オ) | |
| (1) | 正 | オン | 左 | 放電 | 負から正 |
| (2) | 負 | オフ | 右 | 充電 | 正から負 |
| (3) | 正 | オン | 左 | 充電 | 正から零 |
| (4) | 零 | オフ | 左 | 充電 | 負から正 |
| (5) | 零 | オフ | 右 | 放電 | 零から正 |
2011年(平成23年)問13 過去問解説
- スイッチS が開いている状態(オフ)のときは、トランジスタ $T_r$ のベースには抵抗 $R_2$ を介して( 正 )の電圧が加わるので、トランジスタ $T_r$ は( オン )となっている。 ベースの電圧 $V_b$ は電源電圧 $V_{CC}$ より低いので、電流 $i$ は図の矢印 “右” の向きに流れてコンデンサ $C$ は充電されている。
- 次に、スイッチSを閉じる(オン)と、その瞬間はコンデンサ $C$ に充電されていた電荷でベースの電圧は負となるので、コレクタの電圧 $V_C$ は瞬時に高くなる。
電流 $i$ は矢印 “( 左 )” の向きに流れ、コンデンサ $C$ は( 放電 )を始め、やがてベースの電圧は( 負から正 )に変化し、コレクタの電圧 $V_C$ は下がる。
答え (1)
2013年(平成25年)問18
図は、NOT IC、コンデンサ C 及び抵抗を用いた非抵抗マルチバイブレータの原理図である。次の(a)及び(b)の問に答えよ。
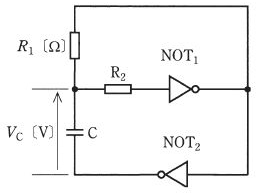
(a) この回路に関する三つの記述(ア)~(ウ)について、正誤の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
- この回路は電源を必要としない。
- 抵抗 R1[Ω]の値を大きくすると、発振周波数は高くなる。
- 抵抗器 R2 は、NOT1 に流れる入力電流を制限するための素子である。
(ア) (イ) (ウ)
(1) 正 正 正
(2) 正 正 誤
(3) 正 誤 誤
(4) 誤 正 誤
(5) 誤 誤 正
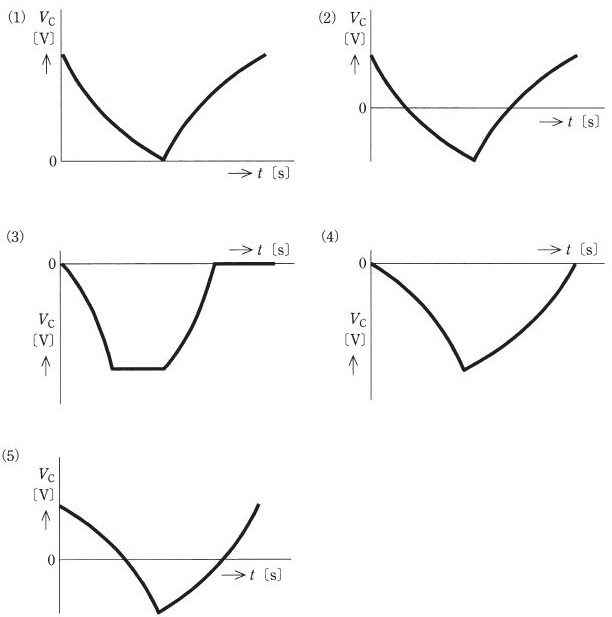
(b) 次の波形の中で、コンデンサCの端子間電圧 Vc[V]の時間 t[s]の経過による変化の特徴を最もよく示している図として、正しいものを次の(1)~(5)のうちから一つ選べ。ただし、いずれの図も1周期分のみを示している。
2013年(平成25年)問18 過去問解説
(a) の解説
- この回路は電源を必要としない。電気回路を動作させるには電源が必要です。したがって誤りです。
- 抵抗 R1[Ω]の値を大きくすると、発振周波数は高くなる。回路の周期は、$R_1$ と $C$ の時定数で決まります。時定数 $τ=CR_1$ が大きいほど、周期は大きくなりますので、発信周波数は低くなります。したがって誤りです。
- 抵抗器 R2 は、NOT1 に流れる入力電流を制限するための素子である。正しい記述です。
答え (5)
(b) この回路は、$R_1$ と $C$ の直れる回路を $NOT_1$ と $NOT_2$ で交互に電圧を加えます。この切替え中ア、過渡現象中となり、時間に対する $V_C$ の変化は曲線の変化が徐々に緩やかになる曲線を描きます。ただし、$V_C$ は定常値になる前に $NOT$ の反転で放電が開始されますので、変化の途中で折れ曲がる曲線になります。この状態を、満たした図は(2)になります。
答え (2)
2016年(平成28年)問18
振幅変調について、次の(a)及び(b)の問に答えよ。
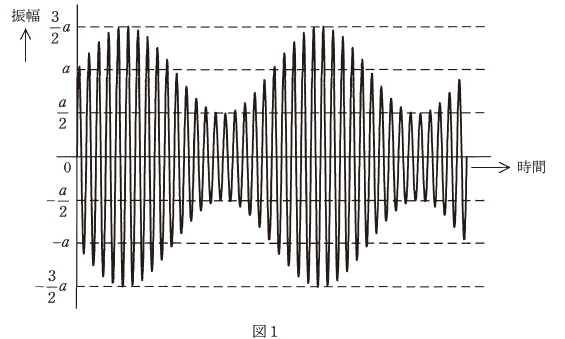
(a) 図1の波形は、正弦波である信号波によって搬送波の振幅を変化させて得られた変調波を表している。この変調波の変調度の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.33 (2) 0.5 (3) 1.0 (4) 2.0 (5) 3.0
(b) 次の文章は、直線検波回路に関する記述である。
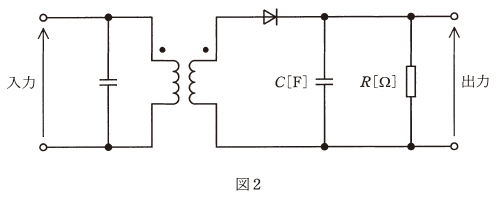
振幅変調した変調波の電圧を、図2の復調回路に入力して復調したい。コンデンサ C [F] と抵抗 R [Ω] を並列接続した合成インピーダンスの両端電圧に求められることは、信号波の成分が( ア )ことと、搬送波の成分が( イ )ことである。そこで、合成インピーダンスの大きさは、信号波の周波数に対してほぼ抵抗 R [Ω] となり、搬送波の周波数に対して十分に( ウ )なくてはならない。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
(ア) (イ) (ウ)
(1) ある なくなる 大きく
(2) ある なくなる 小さく
(3) なくなる ある 小さく
(4) なくなる なくなる 小さく
(5) なくなる ある 大きく
2016年(平成28年)問18 過去問解説
(a) 変調率は次の式で求めることができます。
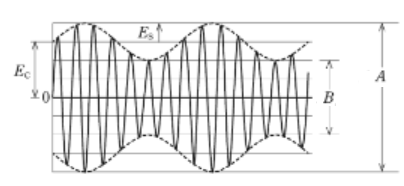
$変調度=\displaystyle\frac{E_S}{E_C}=\displaystyle\frac{A-B}{A+B}$
変調度を$m$とすると、
$m=\displaystyle\frac{\displaystyle\frac{3}{2}a×2-\displaystyle\frac{1}{2}a×2}{\displaystyle\frac{3}{2}a×2+\displaystyle\frac{1}{2}a×2}=0.5$
答え (2)
(b) 振幅変調した変調波の電圧を、図2の復調回路に入力して復調したい。コンデンサ C [F] と抵抗 R [Ω] を並列接続した合成インピーダンスの両端電圧に求められることは、信号波の成分が( ある )ことと、搬送波の成分が( なくなる )ことである。そこで、合成インピーダンスの大きさは、信号波の周波数に対してほぼ抵抗 R [Ω] となり、搬送波の周波数に対して十分に( 小さく )なくてはならない。
答え (2)





